[MPI] 사다리꼴 공식 (trapezoidal rule) 병렬화

References

An Introduction to Parallel Programming

Trapezoidal rule 병렬화
I/O의 처리

사다리꼴 공식 (trapezoidal rule)

이번에는 MPI를 사용하여 사다리꼴 공식(trapezoidal rule)을 병렬화해보도록 하겠습니다.

사다리꼴 공식은 적분을 근사하는 수치적분 방법인데, 적분이 나타내는 넓이를 일련의 사다리꼴들의 넓의의 합으로 근사합니다. (참고 : 위키백과)

우리는 이 사다리꼴 규칙을 사용하여 \(y = f(x)\)라는 함수에 대한 그래프 사이의 영역에 대한 넓이의 근사값을 구해볼 것입니다.

기본적인 아이디어는 x축의 내부를 n개의 동일한 서브인터벌(subinterval)로 구분합니다. 그리고, 그래프와 각 서브인터벌 사이에 존재하는 사다리꼴의 영역의 넓이에 대한 근사값을 구합니다.

그림 (b)에서 나눈 사다리꼴 중의 하나를 가져와서 살펴보겠습니다.

서브인터벌의 끝점을 \(x_i\)와 \(x_{i+1}\)이라고 하면, 이 서브인터벌의 길이 h는 \(x_{i+1} - x_i\) 입니다. 또한, 양끝 수직선의 길이는 \(f(x_i)\)와 \(f(x_{i+1})\)입니다. 따라서, 이 사다리꼴 하나의 넓이는 다음과 같습니다.

\[\text{Area of one trapezoid } = \frac{h}{2} \left [ f(x_i) + f(x_{i+1}) \right ] \]

같은 길이를 갖는 n개의 서브인터벌로 구분했기 때문에 구하고자하는 전체 영역의 양끝을 a, b라고 한다면, h는

\[h = \frac{b - a}{n}\]

으로 구할 수 있습니다. 따라서 왼쪽 끝점을 \(x_0\)이라고 하고, 오른쪽 끝점을 \(x_n\)이라고 한다면 다음과 같은 수식을 만들 수 있습니다.

\[\begin{matrix} x_0 = & a \\ x_1 = & a + h \\ x_2 = & a + 2h \\ \cdots \\ x_{n-1} = & a + (n-1)h\\ x_n = & b \end{matrix}\]

그리고 하나의 사다리꼴 넓이를 구하는 공식을 사용하여 전체 사다리꼴 넓이의 합은 다음과 같이 계산될 수 있습니다.

\[\text{Sum of trapezoid areas } = h \left [ \frac{f(x_0)}{2} + f(x_1) + f(x_2) + \cdots \ f(x_{n-1}) + \frac{f(x_n)}{2} \right ] \]

이 계산 과정을 시리얼 프로그램의 의사 코드로 작성하면 다음과 같습니다.

우리는 이 의사 코드를 다음의 함수로 구현하여 아래에서 사용하도록 하겠습니다 !

double Trap(double a, double b, int n, double h)
{
    double integral;
    
    integral = (f(a) + f(b)) / 2.0;

    for(int k = 0; k < n; k++) {
        integral += f(a + k*h);
    }
    integral = integral * h;

    return integral;
}

시리얼 프로그램으로 구현

우선 위 사다리꼴 공식을 시리얼 프로그램으로 작성해보도록 하겠습니다. 함수 f는 \(f(x) = x^2\)을 사용합니다.

#include <stdio.h>
#include <stdlib.h>

double f(double x);
double Trap(double a, double b, int n, double h);

int main(int argc, char** argv)
{
    double integral;
    double a, b;
    int n;
    double h;

    if (argc != 4) {
        fprintf(stderr, "usage: %s <a> <b> <n>\n", argv[0]);
        fprintf(stderr, "   a: left end-point\n");
        fprintf(stderr, "   b: right end-point\n");
        fprintf(stderr, "   n: the number of subinterval\n");
        exit(-1);
    }

    a = atof(argv[1]);
    b = atof(argv[2]);
    n = atoi(argv[3]);

    h = (b-a)/n;
    integral = Trap(a, b, n, h);

    printf("With n = %d trapezoids, our estimate\n", n);
    printf("of the integral from %f to %f = %.15f\n", a, b, integral);

    return 0;
}

double Trap(double a, double b, int n, double h)
{
    double integral;
    
    integral = (f(a) + f(b)) / 2.0;

    for(int k = 0; k < n; k++) {
        integral += f(a + k*h);
    }
    integral = integral * h;

    return integral;
}

double f(double x)
{
    return x*x;
}

간단하게 위와 같이 구현할 수 있겠네요.

컴파일하고 적절한 argument를 입력하여 실행하면,

0에서 3까지 1024등분으로 나누어서 사다리꼴 공식을 적용하여 그래프 영역의 넓이를 구하면 약 9의 결과를 얻을 수 있습니다. 간단히 \(x^2\)을 0~3까지 적분하면, 3이 나오기 때문에 근사치를 적절하게 구한 것으로 판단됩니다.

사다리꼴 공식의 병렬화

병렬 프로그램의 다음 4개의 기본 과정을 사용하여 설계할 수 있습니다.

문제의 솔루션을 task로 분할한다.
task 간의 통신 채널을 식별한다.
각 task를 composite tasks로 묶는다.
각 composite tasks를 코어(프로세스)에 매핑한다.

파티셔닝 단계에서 우리는 보통 가능한 한 많은 태스크를 사용하려고 시도합니다. 이 사다리꼴 공식에서는 두 종류의 태스크를 사용할 수 있습니다. 하나는 한 개의 사다리꼴의 영역을 찾는 것이고, 다른 하나는 이 영역들의 합을 구하는 것입니다. 따라서 통신 채널은 아래 그림처럼 첫 번째 태스크를 두 번째 하나의 태스크로 합치면 됩니다.

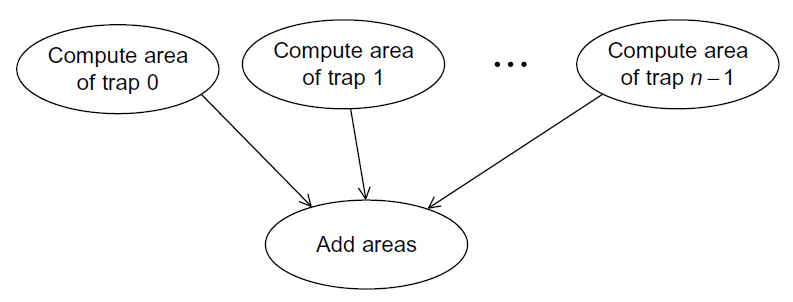
그렇다면 어떻게 태스크를 합치고 이를 각 코어에 매핑할 수 있을까요? 사용하는 사다리꼴이 많으면 많을수록 계산값은 더 정확해지고, 이는 코어 수보다 더 많은 사다리꼴을 사용한다는 것을 의미할 수 있습니다. 그러므로 사다리꼴의 영역에 대한 계산을 그룹으로 묶어야 하는데, 이를 위해서 일반적인 방법은 내부 [a, b]를 comm_sz, 즉 사용가능한 프로세스의 수로 나누는 것입니다. 만약 n이 comm_sz로 나누어서 떨어진다면, 우리는 각 comm_sz개의 서브인터널에서 n/comm_sz개의 사다리꼴에 공식을 간단히 적용할 수 있습니다. 그리고 마지막에 하나의 프로세스 0에서 각 결과를 더합니다.

comm_sz가 n으로 나누어 떨어진다고 가정하고 프로그램을 작성하면 의사코드는 다음과 같이 작성될 수 있습니다.

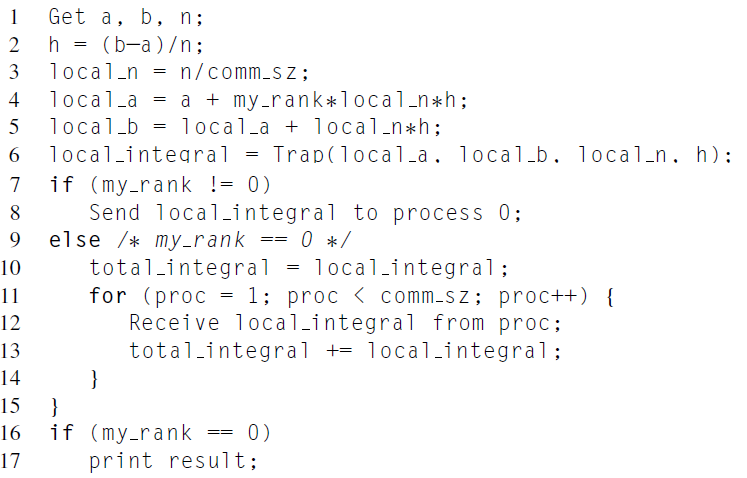
이를 MPI 코드로 작성하면, 다음과 같이 작성할 수 있습니다. 이때, a는 0, b는 3, n은 1024로 프로그램 내에서 하드코딩하였습니다.

(전체 코드 : https://github.com/junstar92/parallel_programming_study/blob/master/mpi/02_mpi_trap1.c)

double Trap(double a, double b, int n, double h);
double f(double x);

int main(void)
{
    int my_rank, comm_sz, n = 1024, local_n;
    double a = 0.0, b = 3.0, h, local_a, local_b, local_int, total_int;

    MPI_Init(NULL, NULL);
    MPI_Comm_size(MPI_COMM_WORLD, &comm_sz);
    MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);

    h = (b-a)/n;
    local_n = n/comm_sz;

    local_a = a + my_rank*local_n*h;
    local_b = local_a + local_n*h;
    local_int = Trap(local_a, local_b, local_n, h);

    if (my_rank != 0) {
        MPI_Send(&local_int, 1, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
    }
    else {
        total_int = local_int;
        for (int source = 1; source < comm_sz; source++) {
            MPI_Recv(&local_int, 1, MPI_DOUBLE, source, 0,
                    MPI_COMM_WORLD, MPI_STATUS_IGNORE);
            total_int += local_int;
        }
    }

    if (my_rank == 0) {
        printf("With n = %d trapezoids, our estimate\n", n);
        printf("of the integral from %f to %f = %.15f\n", a, b, total_int);
    }

    MPI_Finalize();

    return 0;
}

위 코드에서 로컬 변수와 글로벌 변수를 구분했습니다. 로컬(local) 변수는 로컬 변수를 사용하는 프로세스에서만 의미가 있는 변수이고, 이 프로그램에서 local_a, local_b, local_n이 이에 해당합니다. 모든 프로세스에서 의미가 있는 변수는 글로벌(global) 변수이고, 사다리꼴 공식의 a, b, n이 이에 해당합니다.

위 코드를 컴파일하고 실행하면 다음의 결과를 얻을 수 있습니다.

I/O의 처리

물론 위 버전의 사다리꼴 공식의 코드는 문제점이 하나 있는데, 바로 a, b, n이 하드코딩되어 변경이 불가능하다는 점입니다. 코드를 수정하여 3개의 수를 입력받는 프로그램으로 수정할텐데, 입력에 대해 논의하기 전에 먼저 출력에 대해 살펴보도록 하겠습니다.

출력

2021.11.08 - [프로그래밍/병렬프로그래밍] - [MPI] Hello, MPI

[MPI] Hello, MPI

References An Introduction of Parallel Programming Contents MPI (Message-Passing Interface) MPI 프로그램(MPI_Init, MPI_Finalize, Communicator, MPI_Comm_size, MPI_Comm_rank) SPMD 프로그램 communicati..

junstar92.tistory.com

이전 글에서 greeting을 출력하는 프로그램과 위에서 구현한 프로그램은 프로세스 0이 stdout에 결과를 출력한다고 가정했고, 그 작업은 printf를 호출하여 이루어졌습니다. MPI 표준에서는 어떤 프로세스가 어떤 I/O 디바이스를 액세스하도록 설정할 수는 없지만, 보편적으로 MPI_COMM_WORLD에 있는 모든 프로세스들은 stdout과 stderr를 모두 액세스 가능하고 따라서 대부분의 MPI 구현은 모든 프로세스들이 printf와 fprintf(stderr, ...)을 실행할 수 있습니다.

그러나 이러한 디바이스를 액세스하는 작업을 위한 자동 스케줄링은 제공하지 않습니다. 이 말은 여러 프로세스들이 동시에 stdout에 작업하려고 시도하면 어떤 프로세스의 출력이 나타날지 그 순서를 예측할 수가 없습니다. 실제로 한 프로세스의 출력은 다른 프로세스의 출력에 의해 인터럽트될 수도 있습니다.

예를 들어, 각 프로세스가 간단하게 메세지를 출력하는 아래의 MPI 프로그램을 실행해봅시다.

#include <stdio.h>
#include <mpi.h>

int main(void)
{
    int my_rank, comm_sz;

    MPI_Init(NULL, NULL);
    MPI_Comm_size(MPI_COMM_WORLD, &comm_sz);
    MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);

    printf("Proc %d of %d > Done anyone have a toothpick?\n", my_rank, comm_sz);

    MPI_Finalize();

    return 0;
}

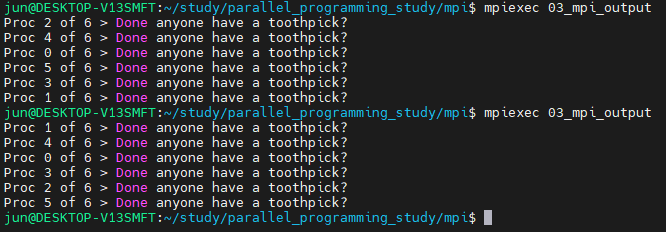
6개의 프로세스를 실행했을 때, 출력 순서를 전혀 예측할 수 없다는 것을 볼 수 있습니다. 이러한 일이 발생하는 이유는 MPI 프로세스들이 출력 디바이스인 stdout을 액세스하기 위해 경쟁하기 때문입니다. 따라서 어떤 프로세스의 결과가 어떤 순서로 출력될지 예측하는 것은 불가능합니다. 이러한 경쟁은 비결정론(nondeterminism)의 결과이며, 실제로 결과는 실행할 때마다 달라집니다.

여러 개의 프로세스들이 무작위로 순서로 출력되는 것을 원치 않는다면 그에 대한 프로그램의 수정의 개발자의 몫입니다. 예를 들어, greeting 프로그램처럼 프로세스 0이 아닌 다른 프로세스들이 프로세스 0에게 출력을 전송하고 프로세스 0은 전송한 프로세스의 rank 순서를 보고 결과를 출력할 수 있습니다.

입력

출력과 달리 대부분의 MPI의 구현에서는 MPI_COMM_WORLD의 프로세스 0이 stdin을 액세스하도록 합니다. 여러 프로세스들이 stdin을 액세스한다면 어떤 프로세스가 어떤 데이터를 입력받는지 예측하기가 힘듦니다.

따라서 scanf를 사용하는 MPI 프로그램을 작성하기 위해서는 프로세스 rank에 따라서 다르게 적용해야 하는데, 프로세스 0이 데이터를 읽고나서 그 데이터를 다른 프로세스에게 전송하도록 해야합니다.

위의 사다리꼴 공식 병렬화 프로그램에서 Get_input 함수를 작성해보겠습니다. 이 함수에서 프로세스 0은 간단하게 변수 a, b, 그리고 n의 값을 읽어오고, 이 3개의 값을 다른 프로세스에게 전송합니다. 이 함수는 greeting 프로그램에서 사용했던 기본적인 통신 API를 사용합니다. 단지 차이점은 프로세스 0이 다른 프로세스에게 전송하고 다른 프로세스는 수신을 한다는 점만 다릅니다.

(전체 코드 : https://github.com/junstar92/parallel_programming_study/blob/master/mpi/04_mpi_trap2.c)

void Get_input(int my_rank, int comm_sz, double* p_a, double* p_b, int* p_n)
{
    int dest;

    if (my_rank == 0) {
        printf("Enter a, b, and n\n");
        scanf("%lf %lf %d", p_a, p_b, p_n);
        for (dest = 1; dest < comm_sz; dest++) {
            MPI_Send(p_a, 1, MPI_DOUBLE, dest, 0, MPI_COMM_WORLD);
            MPI_Send(p_b, 1, MPI_DOUBLE, dest, 0, MPI_COMM_WORLD);
            MPI_Send(p_n, 1, MPI_INT, dest, 0, MPI_COMM_WORLD);
        } 
    } 
    else { /* my_rank != 0 */
        MPI_Recv(p_a, 1, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD,
            MPI_STATUS_IGNORE);
        MPI_Recv(p_b, 1, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD,
            MPI_STATUS_IGNORE);
        MPI_Recv(p_n, 1, MPI_INT, 0, 0, MPI_COMM_WORLD,
            MPI_STATUS_IGNORE);
    } 
}

그리고, 메인 함수에 아래 코드의 line 10과 같이 입력을 받는 함수를 추가해주고 컴파일 후, 실행해보겠습니다.

void Get_input(int my_rank, int comm_sz, double* p_a, double* p_b, int* p_n);

int main(void)
{
	...
    MPI_Init(NULL, NULL);
    MPI_Comm_size(MPI_COMM_WORLD, &comm_sz);
    MPI_Comm_rank(MPI_COMM_WORLD, &my_rank);

    Get_input(my_rank, comm_sz, &a, &b, &n);

    h = (b-a)/n;
    local_n = n/comm_sz;

    ...
}

프로세스 0에서만 입력을 받고, 나머지 프로세스에게 정상적으로 전달되어 넓이를 잘 계산하고 있습니다.

이 사다리꼴 공식 프로그램을 살펴보면, 몇 가지 성능을 향상시킬 수 있는 부분을 발견할 수 있습니다. 가장 확실한 부분은 각 프로세스가 넓이를 연산한 후에 통합하는 "global sum" 부분입니다. rank가 0보다 큰 프로세스들은 작업을 끝낸 후 프로세스 0에게 그 숫자를 전달하고, 프로세스 0은 모든 작업 결과를 global sum에 더합니다.

이때, 다른 프로세스는 거의 아무것도 하지 않습니다. 성능을 향상시키기 위해서 이것보다 더 적합한 작업 분배 방식을 고안할 수 있는데, 이는 다음 글에서 알아보도록 하겠습니다 !

전체 코드는 아래의 github에서 확인하실 수 있습니다.

https://github.com/junstar92/parallel_programming_study

GitHub - junstar92/parallel_programming_study

Contribute to junstar92/parallel_programming_study development by creating an account on GitHub.

github.com

'프로그래밍 > 병렬프로그래밍' 카테고리의 다른 글

[MPI] 행렬 - 벡터 곱 연산 + 성능 평가 (0)	2021.11.12
[MPI] 데이터 분산 (벡터합 병렬화) (0)	2021.11.11
[MPI] 사다리꼴 공식 (trapezoidal rule) 병렬화 - 2 (0)	2021.11.10
[MPI] Hello, MPI (0)	2021.11.08
병렬 프로그래밍 (0)	2021.11.07

별준

[MPI] 사다리꼴 공식 (trapezoidal rule) 병렬화 - 1

References

Contents

사다리꼴 공식 (trapezoidal rule)

시리얼 프로그램으로 구현

사다리꼴 공식의 병렬화

I/O의 처리

출력

입력

'프로그래밍 > 병렬프로그래밍' 카테고리의 다른 글

댓글

티스토리툴바

[MPI] 사다리꼴 공식 (trapezoidal rule) 병렬화 - 1

References

Contents

사다리꼴 공식 (trapezoidal rule)

시리얼 프로그램으로 구현

사다리꼴 공식의 병렬화

I/O의 처리

출력

입력

'프로그래밍 > 병렬프로그래밍' 카테고리의 다른 글

관련글

댓글

티스토리툴바