References
- A Survey of Quantization Methods for Efficient Neural Network Inference (link)
Introduction
딥러닝이 급속도로 발전하면서 모델의 크기는 기하급수적으로 커졌고, 이로 인하여 제한된 리소스의 어플리케이션들에 배포하는 것이 불가능해졌다. 즉, 리소스가 제한되는 환경에서 높은 에너지 효율과 정확도로 실시간 추론이 필요한 분야에서 딥러닝을 활용하는데 문제가 된다. 이는 실시간 헬스케어 모니터링, 자율주행, 오디오 분석, 음성 인식 등 다양한 어플리케이션에 큰 영향을 미칠 것으로 예상된다.
최적의 정확도와 함께 효율성 및 실시간성을 달성하기 위한 많은 연구가 이루어지고 있다. 이러한 연구는 크게 다음과 같이 분류될 수 있다.
- Designing efficient NN model architectures
micro-architecture(e.g., kernel types such as depthwise conv or low-rank factorization)와 macro-architecture(e.g., modeul types such as residual, or inception) 측면에서 신경망 모델 아키텍처를 최적화하는 연구이다. 고전적인 기법은 확장이 불가능한 manual search를 통해 새로운 아키텍처 모듈을 탐색하는 것이 대부분이었다.
최근에는 Automated Machine Learning (AutoML)과 Neural Architecture Search (NAS) 기법이 연구되고 있다. 이러한 기법은 주어진 모델의 size, depth, width 제약 내에서 자동화된 방식으로 적절한 아키텍처를 찾는 것을 목표로 한다.
(Neural Architecture Search: A Survey 참조) - Co-designing NN architecture and hardware together
위와 또 다른 연구로는 목표로 하는 하드웨어 플랫폼을 위한 신경망 아키텍처를 찾는 연구가 있다. 이 연구가 중요한 이유는 신경망 구성 요소의 latency 및 energy 측면의 오버헤드가 하드웨어 의존적이기 때문이다. 예를 들어, 전용 캐시 계층 구조가 있는 하드웨어는 이러한 캐시 계층이 없는 하드웨어보다 bandwidth-bound 연산을 훨씬 효율적으로 수행할 수 있다. 초기의 연구 접근 방식은 마찬가지로 수작업으로 설계하는 것이었으며, 최근에는 AutoML, NAS 기법으로 연구되고 있다. - Pruning
Pruning(가지치기)는 신경망의 메모리 공간과 계산 비용을 줄이는 기법이다. 이 기법을 통해 민감하지 않은 작은 뉴런이 제거되어 sparse computation graph가 만들어진다. 여기서 민감하지 않은 작은 뉴런은 제거해도 모델의 결과나 손실 함수에 영향을 최소한으로 미치는 뉴런을 의미한다 (neurons with small saliency로 지칭).
Unstructured pruning 기법을 사용하면 위치에 상관없이 불필요한 뉴런이 제거된다. 이 방법을 공격적으로 적용하면 모델의 generalization 성능에 거의 영향을 주지 않으면서 대부분의 신경망 파라미터를 제거할 수 있다. 그러나 이 방식은 결국 sparse matrix operations으로 이어지며, 이는 가속하기 어렵다 (일반적으로 memory-bound).
반면, structured pruning 기법을 사용하면 파라미터 그룹이 제거된다. 예를 들어, 전체 convolutional filters가 이에 해당된다. 이 기법을 활용하면 레이어의 입력 및 출력의 모양과 가중치 행렬을 변경하는 효과가 있어 여전히 dense matrix operations를 허용한다. 그러나 공격적으로 적용하면 정확도가 크게 저하되는 경우가 많다. 정확도를 유지하면서 높은 수준의 pruning/sparsity로의 학습 및 추론은 아직 연구 중이다. - Knowledge distillation
Model Distillation은 큰 모델을 학습하고 이를 teacher로 사용하여 더 압축된 모델(student)을 학습하는 기법이다. 이 기법의 핵심은 Student 모델을 학습할 때, 'hard' class labels를 사용하는 것이 아닌 teacher가 생성한 'soft' 확률을 활용하는 것이다. 이러한 확률에는 입력에 대한 더 많은 정보가 포함될 수 있기 때문이다. 여기서의 주요 도전 과제는 distillation 자체 만으로도 높은 압축비를 달성하는 것이다.
INT8 또는 더 낮은 정밀도로 4배의 압축으로 성능을 유지할 수 있는 quantization 및 pruning과 비교했을 때, knowledge distillation 방법은 공격적인 압축으로 무시할 수 없을 정도의 정확도가 저하되는 경향이 있지만, quantization과 pruning을 결합했을 때 성공적일 수 있다는 것을 보여주는 연구가 있다. - Quantization
Quantization(양자화)는 신경망 모델의 학습과 추론 모두에서 성공적인 기법이다. 대부분 추론에 초점을 맞추고 있지만, 이 기법의 놀라운 성과는 학습에서도 적용된다는 것이다. 특히 half-precision과 mixed-precision 학습은 AI 가속기에서 훨씬 더 높은 처리량을 가능하게 한 주요 성과이다. 그러나 상당한 튜닝(tuning)없이 half-precision보다 더 낮은 정밀도를 사용하는 것은 매우 어렵고, 최근 연구의 대부분은 추론에 중점을 두고 있다. - Quantization and Neurosicence
인간의 두뇌가 정보를 연속적인 형태가 아닌 discrete/quantized form으로 저장한다는 것을 신경망의 양자화와 연관지어 연구하고 있다. 이러한 아이디어는 연속적인 형태로 저장된 정보는 필연적으로 노이즈에 의해 손상되는 것에 근거한다. 하지만, 이산적인 표현에서는 이러한 낮은 수준의 노이즈에 더 강력할 수 있다.
Basic Concepts of Quantization
Problem Setup and Notations
신경망(Neural Network; NN)은 \(\{W_1, W_2, \dots, W_L\}\)로 표기되는 학습 가능한 파라미터를 가진 \(L\)개의 레이어를 가지고 있다고 가정하고 \(\theta\)를 모든 파라미터 조합을 표기할 때, supervised learning 문제의 목표는 아래의 empirical risk minimization function을 최적화하는 것이다.

사용되는 Notations의 의미는 다음과 같다.
- \((x, y)\) : the input and the cooresponding label
- \(l(x, y;\theta)\) : loss function (e.g., Mean Squared Error or Cross Entropy Loss)
- \(N\) : the total number of data points
- \(h_i, a_i\) : the input hidden activations of the \(i^{\text{th}}\) layer and corresponding output hidden activation
Quantization에서의 목표는 모델의 generalization power와 accuracy에 최소한의 영향을 미치면서 학습된 모델 파라미터 \(\theta\)와 intermediate activation \(h_i, a_i\)를 low-precision으로 매핑하는 것이다. 이를 위해 floating point를 quantized point로 매핑하는 quantization operator를 정의할 필요가 있다.
Uniform Quantization
Quantization operation 함수는 floating point에서의 실수를 취해 아래 그림과 같이 더 낮은 정밀도 범위로 매핑한다.

흔히 사용되는 quantization function은 다음과 같이 정의된다.
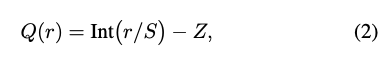
- \(Q\) : quantization operator
- \(r\) : a real valued input (activation or weight)
- \(S\) : a real valued scaling factor
- \(Z\) : an integer zero point
- \(\text{Int}\) : the function that maps a real value to an integer value through a rounding operation (e.g., round to nearest and truncation)
이와 같은 quantization 기법을 uniform quantization이라고 부르며, 결과로 얻어지는 quantized values는 균등하게 분포된다. non-uniform quantization 기법도 있으며, Figure 1의 오른쪽 그림과 같이 매핑되는 값의 분포가 균등하지 않은 것을 확인할 수 있다. non-uniform quantization은 아래에서 더 자세히 다룬다.
실수값을 정수값으로 변환한 뒤, 다시 양자화된 값 \(Q(r)\)로부터 실수값 \(r\)로 복원할 수 있다. 이러한 연산을 dequantization이라고 부른다.

복원된 실수 값 \(\tilde{r}\)는 rounding operation 때문에 \(r\)과 정확히 동일하지 않다는 것에 주의해야 한다.
Symmetric and Asymetric Quantization
Uniform quantization에서 한 가지 중요한 것은 scaling factor \(S\)를 어떻게 선택하느냐이다. \(S\)는 아래와 같이 정의된다.

- \([\alpha, \beta]\) : the clipping range, a bounded range that we are clipping the real values with
- \(b\) : the quantization bit width
따라서, scaling factor를 정의하기 위해서는 먼저 clipping range \([\alpha, \beta]\)를 먼저 결정해야 한다. Clipping range를 결정하는 방법은 보통 calibration이라고 불린다.
가장 단순한 방법은 입력의 min/max를 사용하는 것이다. 즉, \(\alpha = r_{\min}\), \(\beta = r_{\max}\)이다. 이러한 접근 방식을 asymmetric quantization이라고 하며, clipping range가 원점으로부터 비대칭이다 (\(-\alpha \neq \beta\)). 아래 Figure 2의 오른쪽 그림이 이에 해당한다.
Symmetric quantization은 \(\alpha = -\beta\), 즉, clipping range이 대칭이 되도록 선택한다. 일반적으로 \(-\alpha = \beta = \max(|r_{\max}|, |r_{\min}|)\) 식으로 결정한다. 아래 Figure 2의 왼쪽 그림이 이에 해당한다. (2) 식에서 zero point가 \(Z = 0\)이 되므로 quantization 함수가 간단해진다는 장점이 있다.

Asymmetric quantization은 symmetric quantization과 비교했을 때, clipping range가 더 좁아지는 경우가 많다. 이는 target weights 또는 activations가 불균형적일 때 특히 중요하다. 예를 들면, 항상 음수 값이 없는 ReLU 이후의 activation이 있다.
Symmetric Quantization에는 scaling factor를 선택하는 두 가지 옵션이 있다:
- 'full range' symmetric quantization
- 'restricted range' symmetric quantization
Symmetric quantization의 \(S\)는 \(\frac{2\max{(|r|)}}{2^n - 1}\) (with floor rounding mode)로 선택되는데, INT8로 양자화되는 경우, full INT8 range는 [-128, 127] 범위를 사용하고 restricted range는 [-127, 127]를 사용한다. 물론, full range에서 더 정확하다.
Range Calibration Algorithms: Static vs Dynamic Quantization
Clipping range \([\alpha, \beta]\)를 결정하는 여러 가지 calibration 방법이 있지만, 언제 clipping range이 결정되는 시점 또한 매우 중요하다. 대부분 모델의 파라미터는 추론 중에서는 고정되므로 이 범위는 weights에 대해서 정적(static)으로 계산될 수 있다. 그러나 activation map은 각 입력 샘플에 따라 다르다. 따라서, activation을 양자화하는 방법에는 dynamic quantization과 static quantization, 두 가지 기법이 있다.
- dynamic quantization
런타임에 각 activation map에 대해 range를 동적으로 계산한다. 이는 signal statistics(min, max, percentile, ...)의 real-time computation을 요구하므로 오버헤드가 매우 크다. 그러나, 각 입력에 대해서 범위가 정확히 계산되므로 높은 정확도를 얻을 수 있다. - static quantization
미리 계산된 clipping range를 추론에 사용한다. 추가적인 연산 오버헤드가 없지만, dynamic quantization과 비교했을 때 정확도가 더 낮다. 널리 사용되는 방법 중 하나는 일련의 calibration inpus을 사용하여 일반적인 activation ranges를 계산하는 것이다.
양자화되지 않은 원래의 weight 분포와 이에 대응되는 양자화된 값 사이의 MSE를 최소화하는 것을 포함한 여러 메트릭이 사용될 수 있다. 가장 일반적으로는 MSE를 사용하지만 엔트로피(entropy)와 같은 방식을 고려할 수 있다.
이 외의 다른 방식으로는 학습 중에 clipping range를 학습하는 것이 있다.
Quantization Granularity
대부분의 컴퓨터 비전 영역에서 레이어에 대한 activation input은 아래 Figure 3과 같이 여러 개의 다른 convolutional filetes에 의해 연산된다. 각 convolutional filter는 서로 다른 범위의 값을 가질 수 있다.

따라서, 양자화 방법의 한 가지 차별되는 요소는 clipping range \([\alpha, \beta]\)가 계산되는 세분성(granularity)이다. 이 세분성은 다음과 같이 분류된다.
- Layerwise Quantization : 레이어의 전체 convolutional filters의 weights를 고려하여 clipping range가 결정된다. 즉, 해당 레이어의 전체 파라미터의 통계를 검사하고 모든 fliters에 대해 동일한 clipping range를 사용한다. 구현은 매우 간단하지만, 각 filter의 범위가 다를 수 있으므로 최적의 정확도가 아닌 경우가 많다. 예를 들어, 더 좁은 범위의 파라미터를 갖는 convolutional kernel은 더 넓은 범위의 kernel로 인해서 quantization resolution을 잃을 수 있다.
- Groupwise Quantization : 레이어 내 여러 개의 서로 다른 채널을 그룹화한다. 이 방식은 단일 convolution 및 activation에 대한 파라미터의 분포가 많이 다른 경우에 도움이 될 수 있다. 그러나 필연적으로 다양한 scaling factors를 고려해야 하는 연산 비용이 추가된다.
(이 접근 방식은 fully-connected attention layers로 구성된 트랜스포머 모델을 양자화하는 Q-BERT에서 효과적인 것으로 알려졌다) - Channelwise Quantization : Figure 3의 가장 오른쪽에 표시된 것처럼 다른 채널과 관계없이 각 convolution filters에 대해 고정된 값을 사용하는 것이다. 즉, 각 채널마다 scaling factor가 있다. 이를 통해 더 좋은 quantization resolution을 보장하며, 종종 더 높은 정확도를 달성할 수 있다.
- Sub-channelwise Quantization : 각 filter 내에서도 파라미터를 그룹화하여 clipping range를 결정하는 것이다. 다양한 scaling factor를 고려해야 하므로 상당한 오버헤드가 추가될 수 있다.
Channelwise quantization이 현재 convolutional kernel을 양자화하는 표준 방법이다. 이를 통해 무시할 수 있는 오버헤드로 개별 커널의 clipping range를 조정할 수 있다. 반면, sub-channelwise quantization은 상당한 오버헤드가 발생할 수 있다.
Non-Uniform Quantization
Non-uniform quantization은 real values로부터 quantized values의 매핑에서 각 구간이 비균등한 양자화 방법이다. Figure 1의 오른쪽 그림이 이에 해당한다. Non-uniform quantization 공식의 정의는 다음과 같다.

- \(X_i\) : the discrete quantization levels
- \(\Delta_i\) : the quantization steps (thresholds)
실수 \(r\) 값이 \(\Delta_i\)와 \(\Delta_{i+1}\) 사이에 있을 때, quantizer Q는 이를 대응하는 quantization level \(X_i\)로 project한다. \(X_i\)와 \(\Delta_i\)의 간격은 일정하지 않다.
이 방식은 고정된 bit-width에 대해 더 높은 정확도를 얻을 수도 있는데, 더 중요한 값 영역에 집중하거나 적절한 dynamic ranges를 찾음으로써 분포를 더 잘 포착하기 때문이다. 예를 들어, 많은 non-uniform quantization 방법은 종종 long tails를 포함하는 bell-shaped 분포의 weights와 activations를 위해 설계되었다.
일반적인 rule-based non-uniform quantization은 logarithmic distribution(로그 분포)을 사용하는 것이다 (quantization step과 level이 선영이 아닌 기하급수로 증가).
다른 방법으로는 binary code-based quantization이 유명하다. 이 방식은 real vector \(\mathbf{r} \in \mathbb{R}^n\)를 \(m\) binary vectors로 양자화한다.
- \(\mathbf{r} \approx \sum_{i=1}^{m}\alpha_i \bold{b}_i\)
- \(\alpha_i \in \mathbb{R}\) : scaling factor
- \(\bold{b}_i \in \{ -1, +1 \}^n\) : binary vectors
\(\mathbf{r}\)과 \(\sum_{i=1}^{m}\alpha_i \bold{b}_i\) 간의 error를 최소화하기 위한 closed-form solution이 없기 때문에 기존 연구는 휴리스틱한 솔루션에 의존한다. Quantizer를 더 향상시키기 위해서 최근에는 non-uniform quantization을 optimization problem으로 보고, 아래의 식처럼 원본 텐서와 양자화된 텐서 간의 차이를 최소화하도록 \(Q\)의 quantization steps/levels를 조정하는 연구도 있다.

또한, quantizer 자체도 모델 파라미터와 함께 학습될 수 있다. 이 방법을 learnable quantizers라고 부르며, iterative optimization 또는 gradient descent로 quantization steps/levels가 학습된다.
추가로 클러스터링(clustering)은 양자화로 인한 정보 손실을 완화하는데 도움이 될 수 있다. 일부 연구에서는 quantization steps와 levels를 결정하기 위해 다양한 텐서에서 k-means를 사용하고, 일부 다른 연구에서는 성능 손실을 최소화하기 위해 weights에 Hessian-weighted k-means clustering을 적용한다.
일반적으로 non-uniform quantization을 사용하면 파라미터 범위를 불균일하게 범위를 구분하여 신호 정보를 더 잘 캡처할 수 있다. 하지만, 일반적으로 CPU나 GPU에서 효율적으로 배포하기가 어렵다. 현재는 단순성과 하드웨어에 대한 효율적인 배포로 인해 사실상 uniform-quantization이 지배적이다.
Fine-tuning Methods
양자화 이후에 신경망의 파라미터를 조정해야 하는 경우가 많다. 이는 Quantization-Aware Training(QAT)라고 불리는 프로세스로 모델을 다시 학습하여 수행되거나, Post-Training Quantization(PTQ)라고 하는 프로세스로 재학습없이 수행될 수 있다. 이 두 가지 접근 방식의 비교는 아래 그림에서 간단하게 보여주고 있다.

Quantization-Aware Training (QAT)
학습된 모델이 주어졌을 때, quantization은 학습된 모델의 파라미터를 오염시켜 부동소수점 정밀도로 훈련되었을 때 수렴되었던 지점으로부터 멀어질 수 있다. 이는 loss가 더 적은 지점으로 수렴할 수 있도록 양자화된 파라미터로 모델을 재학습함으로써 해결할 수 있다. 널리 사용되는 방법 중 하나가 바로 Quantization-Aware Training (QAT)이다. 이 방법은 부동소수점으로 양자화된 모델에 대해서 forward 및 backward pass가 수행되지만, 모델의 파라미터는 각 gradient가 업데이트된 후에 양자화된다 (similar to projected gradient descent). 가중치 업데이트가 부동소수점으로 수행된 이후에 projection을 수행하는 것이 중요하다. Backward pass도 부동소수점으로 수행하는 것이 중요한데, 양자화된 정밀도로 gradients를 누적하면, 특히 낮은 정밀도에서 높은 에러의 gradients 혹은 zero-gradients가 발생할 수 있기 때문이다.
역전파에서 중요한 것은 미분이 불가능한 quantization operator ((2) 식 참조)가 처리되는 방식이다. 근사가 없다면, 이 연산의 gradient는 (2) 식의 rounding operation(piece-wise flat operator)으로 인해 거의 모든 지점에서 0이다. 이 문제를 해결하는 유명한 접근 방식은 소위 Straight Through Estimator (STE)로 불리는 방식을 통해 기울기를 근사하는 것이다. STE는 rounding operation을 무시하고 아래 그림에서 설명하는 것처럼 identity function을 사용하여 근사한다. 대략적인 근사에도 불구하고 binary-quantization과 같은 초저정밀 양자화를 제외하고는 실제로 잘 동작하는 경우가 많다.

아래와 같은 다른 접근 방식들도 연구되고 있다.
- Stochastic neuron approach
- Combinatorial optimization
- Target propagation
- Gumbel-softmax
- Use regularization operators to enforce the weight to be quantized (referred to as Non-STE methods)
- ProxQuant : removes the rounding operation in the quantization formula (2), and instead uses the so-called W-shape, non-smooth regularization function to enforce the weights to quantized values.
- Using pulse training to approximate the derivative of discontinuous points
- Replacing the quantized weights with an affine combination of floating point and quantized parameters
- AdaRound : an adaptive rounding method as an alternative to round-to-nearest method
많은 연구들이 있지만 위와 같은 방법들에는 많은 튜닝이 필요한 경우가 많으며, 현재까지는 STE가 가장 일반적으로 사용된다.
파라미터를 튜닝하는 것 외에도 QAT 중 quantization parameter를 학습하는 것도 효과적이다.
- PACT : uniform quantization에서 activation의 clipping range를 학습
- QIT : non-uniform quantization setting을 위한 quantization steps 및 levels도 학습
- LSQ : QAT 중에 non-negative activations (e.g., ReLU)에 대한 scaling factor를 학습하기 위한 새로운 gradient estimate 도입
- LSQ+ : 기존 아이디어를 swish 및 h-swish와 같은 일반 activation function으로 확장
Summary. QAT는 STE의 대략적인 근사에도 잘 동작하는 것으로 확인되었다. 하지만 QAT의 주요 단점은 모델을 재학습하는데 드는 비용이다. 특히 낮은 비트의 정밀도에 대한 양자화에서는 정확성을 이전 수준으로 복구하기 위해 수백 epoch 동안 재학습해야 할 수도 있다. 장기간 사용되고 효율성과 정확성이 특히나 중요하다면 가치가 있지만, 모델의 수명이 상대적으로 짧다면 효율적이지 못하다.
Post-Training Quantization (PTQ)
고비용의 QAT 대안으로 사용되는 Post-Training Quantization (PTQ)는 fine-tuning없이 quantization과 weight adjustment를 수행한다. 따라서, PTQ의 오버헤드는 매우 낮고 종종 무시할 수 있다. 또한, 재학습을 위해 충분한 학습 데이터가 필요한 QAT와 달리 PTQ는 데이터가 제한적이거나 label이 지정되지 않은 상황에서도 적용할 수 있다는 장점이 있다. 그러나, 정밀도가 특히 낮은 양자화에서는 QAT에 비해 정확도가 떨어지는 경우가 많다.
이러한 이유로 PTQ의 정확도 감소를 완화하기 위한 다양한 방법들이 제안되었다.
- 양자화에 따른 가중치의 평균과 분산의 고유한 편향을 관측하고 이러한 편향을 보정하는 방법 제안
- 서로 다른 레이어나 채널 간의 weight ranges (and implicitly activation ranges)를 균등화하면 quantization error를 줄일 수 있음을 보여줌
- ACIQ : PTQ에 대한 최적의 clipping range와 channel-wise bitwidth setting을 분석적으로 계산. 정확도 저하가 감소되지만 사용되는 channel-wise activation quantization은 하드웨어에서 효율적으로 사용하기 어렵다.
- OMSE method : ACIQ의 단점을 해결하기 위해 activation에서의 channel-wise quantization을 제거하고 양자화된 텐서와 대응되는 부동소수점 텐서 사이의 L2 distance를 최적화하여 PTQ를 수행하는 것을 제안
- Outlier Channel Splitting (OCS) : outlier가 PTQ에 미치는 부정적인 영향을 완화하기 위해 outlier values를 포함하는 채널을 복제하고 절반으로 줄이는 방법 제안
- AdaRound : naive round-to-nearest 방법이 양자화에서 반직관적으로 sub-optimal solutions을 초래할 수 있음을 보여주고 loss를 더 잘 줄일 수 있는 adaptive rounding method를 제안
- AdaQuant : AdaRound는 양자화된 가중치의 변화를 \(\pm 1\) 이내로 제한하는 반면, AdaQuant는 필요에 따라 양자화된 가중치를 변경할 수 있는 보다 일반적인 방법을 제안
Zero-shot Quantization
지금까지 설명한 방식으로 양자화를 진행한 이후 정확도 감소를 최소화하려면 학습 데이터 일부가 필요하다. 먼저, 값을 clipping하고 적절한 scaling factor를 결정할 수 있도록 activation의 range를 알아야 한다. 그런 다음, 양자화된 모델은 모델 파라미터를 조정하고 정확도 저하를 복구하기 위해 fine-tuning이 필요한 경우가 많다. 그러나 대부분의 프로세스 중에는 원래의 학습 데이터에 접근하는 것이 불가능한 경우가 많다 (데이터셋이 너무 크거나 보안, 개인정보 문제로 인해 사용할 수 없거나). 이 문제를 해결하기 위해 zero-shot quantization (ZSQ)라고 하는 여러 방법들이 제안되었다. 이는 먼저 두 가지 다른 수준의 zero-shot quantization으로 설명할 수 있다.
- Level 1 : No data and no fine-tuning (ZSQ + PTQ)
- Level 2 : No data but requires fine-tuning (ZSQ + QAT)
Level 1은 어떠한 fine-tuning도 없이 빠르고 쉬운 quantization이 가능하다. 반면, fine-tuning이 정확도 감소를 복구하는데 도움이 되므로 일반적으로 Level 2에서 정확도가 더 높다.
관련된 내용은 논문을 참조.
Stochastic Quantization
추론하는 동안, quantization scheme은 보통 결정적(deterministic)이다. 그러나 항상 그런 것은 아니며, 일부 연구에서는 QAT와 감소된 정밀도 학습을 위한 stochastic quantization을 탐구했다. 직관적으로 stochastic quantization을 통해 deterministic quantization에 비해 신경망이 더 많은 탐색을 수행한다는 것을 알 수 있다. 근거 중 하나는 rounding operation이 항상 동일한 가중치를 반환할 수 있으므로 작은 가중치로 인해 가중치 업데이트가 발생하지 않을 수 있다는 것이다. 그러나 stochastic rounding을 사용하면 동일한 작은 가중치에서도 업데이트가 발생할 수 있다.
공식화하면 stochastic quantization은 floating number를 가중치 업데이트의 크기와 관련된 확률을 사용하여 up 또는 down으로 매핑한다. 예를 들어, (2) 식은 다음과 같이 정의된다.

위 정의는 binary quantization에서는 사용될 수 없어서, 아래의 식으로 정의된다.

Binary는 real value \(x\)를 이진화하는 함수이며, \(\sigma(\cdot)\)은 sigmoid 함수이다.
QuantNoise에서는 또 다른 stochastic quantization 방법이 도입되었다. 여기서는 각 forward pass 동안 서로 다른 무작위의 weights의 하위 집합을 양자화하고 unbiased gradients로 모델을 학습한다. 이를 통해 많은 컴퓨터비전 및 자연어처리 모델에서 정확도가 크게 떨어지지 않고 낮은 비트의 정밀도의 양자화가 가능하다. 그러나 이 방식들의 주요 과제는 모든 단일 가중치 업데이트에 대해 난수를 생성하는 오버헤드이므로 널리 사용되지는 않는다.
Advanced Concepts : Quantization Below 8 Bits
Simulated and Integer-only Quantization
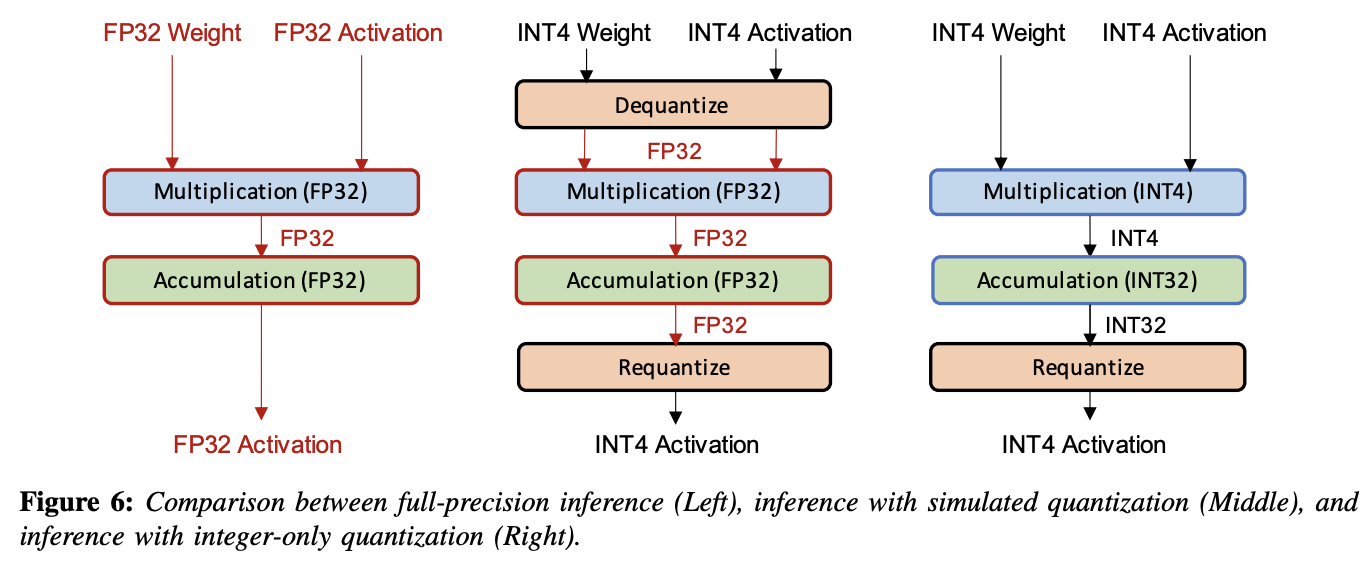
양자화된 신경망 모델을 배포하는 두 가지 일반적인 방법이 있다.
- Simulated quantization (aka fake quantization) : 모델의 파라미터는 낮은 정밀도로 저장하지만 연산은 부동소수점으로 수행한다. 따라서, 양자화된 파라미터는 Figure 6의 중간 그림에서와 같이 부동소수점 연산을 수행하기 전 dequantization 과정이 필요하다. 이로 인해, low-precision logic의 속도와 효율성을 완전히 활용할 수는 없다.
- Integer-only quantization (aka fixed-point quantization) : 모든 연산이 low-precision integer arithmetic으로 수행된다 (Figure 6의 오른쪽 그림). 파라미터나 activation의 floating-point dequantization 없이 효율적인 integer arithmetic을 통해 전체 추론을 수행할 수 있다.
일반적으로 부동소수점 연산을 사용하여 full-precision으로 추론을 수행하면 정확도에 도움이 될 수 있지만, 이는 low-precision logic의 이점을 누릴 수가 없게 된다. low-precision logic은 latency, power consumption, area efficiency 측면에서 여러 가지 이점이 있다. 아래 그림처럼 많은 하드웨어 프로세서는 low-precision arithmetic의 빠른 처리를 지원한다.
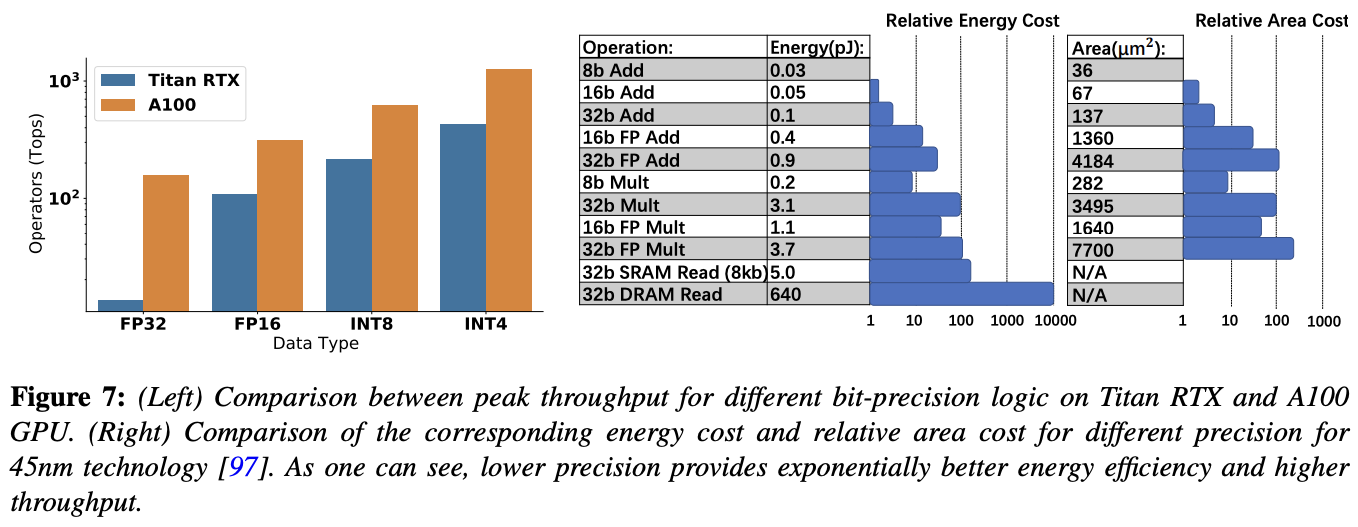
주목할만한 interger-only quantization 연구에는 이전 conv layer에 batch normalization을 fusion하는 것과 batch normalization을 사용하여 residual networks에 대한 integer-only computation을 제안하는 것이 있다. 초기 연구에는 두 방법 모두 ReLU activation으로 제한되지만, 최근 연구에서는 GeLU, Softmax 및 Layer Normalization을 integer arithmetic으로 근사하여 이러한 제한 사항을 해결하고 Transformers 아키텍처로 integer-only quantization을 확장한다.
Dyadic Quantization : integer-only quantization의 다른 종류이다. 모든 scaling은 dyadic numbers로 수행된다. Dyadic number는 분자가 정수이면서 분모는 2의 거듭제곱인 유리수이다. 결과적으로 정수의 addition, multiplication, bit shifting만 필요하고 integer division은 필요없는 연산 그래프가 생성된다. 중요한 점은 이 방식에서 모든 additions (e.g., residual connections)가 동일한 dyadic scale을 갖도록 강제하여 addition logic을 더 높은 효율성으로 심플하게 만들 수 있다는 것이다.
Mixed-Precision Quantization
낮은 정밀도로 양자화하면 하드웨어 성능이 향상된다는 것을 쉽게 알 수 있다. 하지만, 너무 낮은 정밀도로 uniform quantization을 적용하면 정확도가 크게 저하될 수 있다. 이는 mixed-precision quantization으로 해결할 수 있다.

이 방식은 위 그림에서 설명하는 것과 같이 각 레이어가 서로 다른 bit precision으로 양자화된다. 이 방식의 한 가지 문제는 각 레이어의 bit 설정을 선택하기 위한 탐색이 레이어 수에 따라 기하급수적으로 증가한다는 것이다. 이러한 탐색 공간을 해결하기 위해 다양한 방식이 제안되었다.
이는 근본적으로 searching problem이며, 많은 다른 방법들이 제안되었다. 최근 연구에서는 quantization policy를 자동으로 결정하기 위해 강화 학습(reinforcement learning; RL) 기반의 방식을 제안했다. 다른 연구에서는 mixed-precision configuration searching 문제를 Neural Architecture Search (NAS)로 공식화하여 효율적으로 탐색하기 위해 Differentiable NAS (DNAS) 방법을 사용했다. 이러한 탐색 기반 방법의 한 가지 단점은 종종 큰 계산 리소스가 필요하고 성능이 일반적으로 하이퍼파라미터 및 초기화에 민감하다는 것이다.
이외의 다른 방식으로는 periodic function regularization을 사용하여 서로 다른 레이어를 자동으로 구별하고 각 레이어의 정확도에 대한 다양한 중요성을 학습하는 동시에 각각의 bitwidths를 학습하여 mixed-precision model을 학습하는 방법이 있다.
위의 탐색 및 정규화(regularization) 기반 접근 방식과는 달리 HAWQ는 모델의 second-order sensitivity를 기반으로 mixed-precision setting을 찾는 방법을 도입했다 (HAWQv2, HAWQv3로 확장).
Hardware Aware Quantization
Quantization의 목적 중 하나는 inference latency를 개선하는 것이다. 그러나 모든 하드웨어에서 양자화된 이후에 동일한 속도 향상을 제공하는 것은 아니다. 실제로 양자화로 인한 이점은 하드웨어에 따라 다르며, on-chip memory, bandwidth, cache hierarchy 등 많은 요소들이 속도 향상에 영향을 미친다.
Hardware-Aware Quantization을 통해 최적의 향상을 달성하려면 이러한 영향들을 고려하는 것이 중요하다. 한 연구에서는 강화학습 에이전트를 활용하여 서로 다른 bitwidths를 가진 서로 다른 레이어에 대한 latency의 룩업테이블을 기반으로 hardware-aware mixed-precision setting을 결정한다. 하지만 이러한 방식은 simulated hardware latency를 사용한다. 이를 해결하기 위해 최근 연구에서는 quantized operations를 하드웨어에 직접 배포하여 다양한 quantization bit precision에 대한 각 레이어의 실제 latency를 측정한다.
Distillation-Assisted Quantization
Model distillation을 통해 quantization accuracy를 높이는 연구도 있다. Model distillation에서 student 모델을 학습하는 동안 ground-truth class labels를 사용하는 것이 아닌 입력에 대해 더 많은 정보를 포함할 수 있는 teacher가 생성한 soft probabilities를 활용하도록 한다. 즉, 전체 loss function은 student loss와 distillation loss를 모두 포함하여 아래와 같이 공식화된다.

- \(\alpha, \beta\) : weighing coefficients to tune the amount of loss from the student model and the distillation loss
- \(y\) : the ground-truth class label
- \(\mathcal{H}\) : the cross-entropy loss function
- \(z_s, z_t\) : the logits generated by the student and teacher model
- \(\sigma\) : the softmax function
- \(T\) : its temperature defined as belows

Extreme Quantization
이진화(binarization)은 정보를 1비트로 표현하여 메모리 요구 사항을 32배로 줄이는 가장 극단적인 양자화 방법이다. 메모리 이점 이외에도 binary (1-bit) 및 ternary (2-bit) 연산은 bit-wise arithmetic을 통해 효율적으로 계산될 수 있으며, FP32 및 INT8과 같은 더 높은 정밀도에 비해 상당한 가속을 달성할 수 있다. 예를 들어, NVIDIA V100 GPU의 peak binary arithmetic은 INT8의 8배이다. 하지만 naive binarization 방법은 상당한 정확도 하락을 초래할 수 있다. 따라서, 이를 해결하기 위한 많은 연구들이 있다. 이러한 솔루션은 크게 3가지로 분류된다. 자세한 내용은 Binary Neural Networks: A Survey 에서 확인할 수 있다.
- Quantization Error Minimization
- Improved Loss Function
- Improved Training Method
Vector Quantization
Quantization은 머신러닝 분야에서 처음 사용된 것이 아닌, 정보 이론, 특히, 신호 처리 분야에서 압축에 이미 널리 사용되고 있었다. 머신 러닝에서 사용되는 것과의 차이점은 근본적으로 원래 신호와 비교하여 최소환의 변경/에러로 신호를 압축하는 데 관심을 가지는 것이 아니며 가능한 한 작은 loss로 더 낮은 정밀도의 표현을 찾는 것이 목표라는 것이다. 따라서, quantized weights/activations가 non-quantized 버전과 크게 다르더라도 허용된다.
NN quantization, 특히, vector quantization에 적용된 DSP에서의 고전적인 양자화 방법에는 흥미로운 아이디어들이 많다. 한 가지 연구로는 weights를 서로 다른 그룹으로 클러스터링하고 추론 중에 각 그룹의 centroid를 quantized values로 사용한다. 이는 아래의 식으로 정의된다.

- \(i\) : the index of weights in a tensor
- \(c_1, \dots, c_k\) : the \(k\) centroid sfound by the clustering
- \(c_j\) : the corresponding centroid to \(w_i\)
클러스터링 이후에는 weight \(w_i\) 룩업테이블로부터 \(c_j\)와 관련된 클러스터 인덱스 \(j\)를 갖게 된다.
k-means clustering을 사용하면 정확도 저하없이 모델 크기를 최대 8배까지 줄이는 데 충분하다는 것이 연구로 밝혀졌다. 또한 k-mean 기반의 vector quantization을 pruning과 허프만 코딩을 함께 적용하면 모델 크기를 더욱 줄일 수 있다.
Product quantization은 vector quantization의 확장이다. 이 방법은 weight matrix를 submatrices로 나누고, vector quantization을 각 submatrix에 적용한다. 기본적인 product quantization 방법 외에도 클러스터링을 보다 세밀하게 사용하면 정확도가 더욱 향상될 수 있다.
Quantization and Hardware Processors
Quantization을 적용하면 모델의 크기를 줄일 수 있을 뿐만 아니라 낮은 정밀도를 위한 logic을 가진 하드웨어에서 더 빠르고 더 적은 전력 사용을 달성할 수 있다. 따라서, quantization은 IoT 및 모바일 어플리케이션에서 edge deployment에 특히 중요하다. Edge device에는 리소스 제약이 있는 경우가 많으며, deep NN 모델을 충족하기에는 비용이 너무 많이 드는 경우가 많다. 또한, 대부분의 edge device에서는 부동소수점 연산을 지원하지 않는 경우가 많다.
ARM Cortex-M은 low-cost 및 power-efficient 임베디드 장치용으로 설계된 32-bit RISC ARM 프로세서 코어 군이다 (e.g., STM32 family). 일부 ARM Cortex-M 코어에는 부동소수점 유닛이 포함되어 있지 않으므로 모델을 배포하기 전 양자화는 필수이다. CMSIS-NN은 모델을 양자화하고 ARM Cortex-M 코어에 배포하는 ARM의 라이브러리이다. 특히, 2의 거듭제곱의 scaling factor와 함께 fixed-point quantization을 활용하여 quantization 및 dequantization 프로세서를 bit shifting operations으로 효율적으로 수행할 수 있다.
GAP-8은 전용 CNN 가속기로 edge inference를 위한 RISC-V SoC이며 정수 연산만 지원하는 프로세서의 또 다른 예이다.
Google Edge TPU는 데이터 센서에서 사용되는 Cloud TPU와 달리 소형 및 저전력으로 설계되어 8비트 연산만 지원하며, 모델은 Tensorflow의 QAT 또는 PTQ를 사용하여 양자화되어야 한다.

Figure 9는 딥러닝 모델 추론에 널리 사용되는 다양한 엣지 프로세서에 대한 처리량(throughput)을 보여준다.
Future Directions for Research in Quantization
- Quantization Software : 현재 대부분의 소프트웨어에서는 INT8 quantization를 주로 지원하며, 더 낮은 정밀도 및 mixed-precision quantization을 지원하는 소프트웨어가 그리 많지 않다. 따라서 낮은 정밀도의 양자화를 위한 효율적인 소프트웨어 API 개발이 중요하다.
- Hardware and NN Architecture Co-Design : 가능한 하드웨어 구성(e.g., different microarchitectures of multiply-accumulate elements)을 탐색하고 이를 네트워크 아키텍처과 함께 설계되는 것도 유용할 수 있다.
- Coupled Compression Methods : Quantization은 딥러닝 모델을 효율적으로 배포하는 방법 중 하나일 뿐이며, 다른 접근 방식과 결합될 수 있다. 아직 이에 대한 연구는 많지 않다.
- Quantized Training : Quantization의 가장 중요한 용도는 half-precision으로 학습을 가속화하는 것이었다. 이를 통해 학습이 더 빠르고 전력 소모도 효율적으로 수행될 수 있었다. 이를 INT8 precision 학습으로 끌어올리는 것은 아주 어려웠다. 여러 가지 연구들이 있지만 많은 방법들이 많은 하이퍼파라미터 조정이 필요하거나 상대적으로 쉬운 학습인 소수의 모델에만 동작했다. 기본적인 문제는 INT8 precision으로 인해 학습이 불안정해진다는 것이다. 이를 해결하면 edge training에 큰 영향을 미칠 수 있다.
'ML & DL > Study' 카테고리의 다른 글
| Integer Quantization for Deep Learning Inference 리뷰 (0) | 2024.02.07 |
|---|---|
| [선형대수] 특잇값 분해와 유사역행렬 (0) | 2022.05.14 |
| [선형대수] 고윳값 분해 (0) | 2022.05.13 |
| [선형대수] Norm (노름) (0) | 2022.05.13 |
| [선형대수] 일차종속과 생성공간 (0) | 2022.05.12 |


댓글