References
- Deep Learning Book(https://www.deeplearningbook.org/)
- 프리드버그 선형대수학
Contents
- 대각행렬 (diagonal matrix, 대각선 행렬)
- 직교행렬 (orthogonal matrix)
- 고윳값 분해 (eigendecomposition)
대각행렬
대각행렬(diagonal matrix)는 0이 아닌 성분들이 주대각(main diagonal)에만 있고, 나머지 성분들은 모두 0인 행렬입니다. 이를 공식화하여 표현하면, 행렬 \(\boldsymbol{D}\)가 모든 \(i \neq j\)에 대해 \(D_{i, j} = 0\)일 때 행렬 \(\boldsymbol{D}\)를 대각행렬이라고 합니다. 이미 알고 있는 대각행렬이 있을텐데, 주대각 성분들이 모두 1인 단위행렬이 바로 대각행렬입니다. 벡터 \(\boldsymbol{v}\)의 성분들이 주대각 성분들인 정방 대각행렬을 diag(\(\boldsymbol{v}\))로 표기합니다.
대각행렬이 흥미로운 이유 중 한 가지는 대각행렬과 벡터의 곱셈 계산이 아주 효율적이라는 점입니다. diag(\(\boldsymbol{v}\))\(\boldsymbol{x}\)를 계산하려면 그냥 각 \(x_i\)에 \(v_i\)만 곱해주면(비례하면) 됩니다. 다르게 표현하면, diag(\(\boldsymbol{v}\))\(\boldsymbol{x} = \boldsymbol{v} \odot \boldsymbol{x}\)입니다.
역행렬은 모든 주대각 성분이 0이 아닐 때에만 존재합니다. 이 경우에는 diag(\(\boldsymbol{v}^{-1}\)) = diag(\([\frac{1}{v_1}, \cdots, \frac{1}{v_n}]^\top\)) 입니다. 많은 경우, 임의의 행렬들로는 다소 일반적인 머신러닝 알고리즘을 유도할 수 있지만, 일부 행렬이 대각행렬이어야 한다는 제약을 두면 비용이 적은(덜 서술적인) 알고리즘을 얻을 수 있습니다.
대각행렬이 반드시 정방행렬이어야 하는 것은 아닙니다. 직사각형 형태의 대각행렬을 만드는 것도 가능합니다. 비정방 대각행렬에는 역행렬이 없지만, 그래도 곱셈이 효율적입니다. \(\boldsymbol{D}\)가 비정방 대각행렬일 때, 곱 \(\boldsymbol{Dx}\)는 \(\boldsymbol{x}\)의 각 성분을 비례한 후, 만약 \(\boldsymbol{D}\)가 세로로 긴 형태이면 적절한 개수의 0들을 비례한 결과에 덧붙이고, \(\boldsymbol{D}\)가 가로로 긴 형태이면 벡터의 마지막 성분들을 적절히 제거하여 구하면 됩니다.

직교행렬
벡터 \(\boldsymbol{x}\)와 \(\boldsymbol{y}\)가 \(\boldsymbol{x}^\top \boldsymbol{y} = 0\)을 만족할 때, 이러한 두 벡터를 가리켜 서로 직교(orthogonal)한다고 말합니다. 두 벡터가 모두 노름이 0이 아니라면, 두 벡터의 각도는 90도입니다. \(\mathbb{R}^n\)에서 노름이 0이 아니고, 서로 직교인 벡터들은 n개를 넘지 않습니다. 직교일 뿐만 아니라 크기가 단위노름인 벡터를 가리켜 정규직교(orthonormal) 벡터라고 부릅니다.
직교행렬(orthogonal matrix)은 행들이 서로 정규직교이고, 열들도 서로 정규직교인 정방행렬을 말합니다.
\[\boldsymbol{A}^\top \boldsymbol{A} = \boldsymbol{AA}^\top = \boldsymbol{I}\]
위 식은 다음이 성립함을 의미합니다.
\[\boldsymbol{A}^{-1} = \boldsymbol{A}^\top\]
따라서, 직교행렬은 역행렬을 계산하기가 매우 쉬우며, 이 점이 직교행렬을 관심있게 살펴보는 주된 이유입니다.
참고로, 행들과 열들이 그냥 직교가 아닌 완전히 정규직교이어야만 합니다. 행들이나 열들이 정규직교가 아니라 그냥 직교인 행렬을 특별히 부르는 이름은 없습니다.
고윳값 분해
수학적 대상 중에는 이를 구성요소들로 분해하여, 표현 방식과는 무관하게 보편적인 어떤 성질을 찾아내면 더 이해하기 쉬운 것들이 있습니다.
예를 들어, 정수는 소인수(prime factor)들로 분해할 수 있습니다. 12라는 수는 밑(기수)를 10으로 두느냐 2로 두느냐에 따라 십진수 또는 이진수로 표현되지만, 어떤 경우든지 12=2x2x3이라는 사실은 항상 참입니다. 이러한 소인수분해 표현해서 여러 유용한 성질들을 이끌어낼 수 있는데, 12는 5로 나누어지지 않으며 12의 임의의 정수배는 3으로 나누어짐을 알 수 있습니다.
이와 같이 행렬을 다양한 방식으로 분해해 보면 성분들의 배열 형태로 표현된 행렬에서는 미처 발견하지 못한 여러 속성들이 드러납니다.
가장 널리 사용되는 행렬 분해 방법 중 하나는 고윳값 분해(eigendecomposition)입니다. 고윳값 분해에서는 행렬을 일단 고유벡터(eigenvector)와 고윳값(eigenvalue)들로 분해합니다.
정방행렬 \(\boldsymbol{A}\)의 고유벡터는 하나의 0이 아닌 벡터 \(\boldsymbol{v}\)인데, \(\boldsymbol{A}\)와 곱해도 \(\boldsymbol{v}\)의 스케일만 변한다는 조건을 만족합니다.
\[\boldsymbol{Av} = \lambda\boldsymbol{v}\]
위 식에서 스칼라 값 \(\lambda\)를 이 고유벡터에 대응되는 고윳값이라고 부릅니다.
\(\boldsymbol{v}^\top \boldsymbol{A} = \lambda\boldsymbol{v}^\top\)로 정의되는 좌고유벡터(left eigenvector)도 있지만, 일반적으로 딥러닝에서는 우고유벡터만 다룹니다.
\(\boldsymbol{v}\)가 \(\boldsymbol{A}\)의 한 고유벡터이면, 그것을 임의의 \(s \in \mathbb{R}, s \neq 0\)으로 비례한 벡터 \(s\boldsymbol{v}\)도 \(\boldsymbol{A}\)의 한 고유벡터입니다. 더 나아가서, \(s\boldsymbol{v}\)의 고윳값은 \(\boldsymbol{v}\)의 고윳값과 같습니다. 그래서, 일반적으로 비례되지 않은 단위 고유벡터만을 고려합니다.
행렬 \(\boldsymbol{A}\)에 일차독립인 n개의 고유벡터 \(\{\boldsymbol{v}^{(1)}, \cdots, \boldsymbol{v}^{(n)}\}\)이 있고, 이들에 대응되는 고윳값들이 \(\{\lambda_1, \cdots, \lambda_n\}\)이라고 가정해봅시다. 이 고유벡터들을 열마다 하나씩 연결해서 행렬 \(\boldsymbol{V}\)를 만들 수 있습니다. 즉, \(\boldsymbol{V} = [\boldsymbol{v}^{(1)}, \cdots, \boldsymbol{v}^{(n)}]\) 입니다. 마찬가지로, 고윳값들로 하나의 벡터 \(\boldsymbol{\lambda} = [\lambda_1, \cdots, \lambda_n]^\top\)을 만들 수 있습니다.
이때, \(\boldsymbol{A}\)의 고윳값 분해는 다음과 같이 정의됩니다.
\[\boldsymbol{A} = \boldsymbol{V}\text{diag}(\boldsymbol{\lambda})\boldsymbol{V}^{-1}\]
사실, 특정한 고윳값들과 고유벡터들로 행렬을 구축(construction)함으로써 공간을 원하는 방향들로 확장할 수 있습니다. 그러나 이처럼 행렬을 새로 구축하는 것이 아니라 기존 행렬을 고윳값들과 고유벡터들로 분해(decomposition)할 필요가 있는 경우도 많습니다. 정수를 소인수들로 분해하면 그 정수를 이해하는 데 도움이 되는 것처럼, 행렬을 분해하면 행렬의 특정 성질을 분석하는 데 도움이 됩니다.
모든 행렬을 고윳값들과 고유벡터들로 분해할 수 있는 것은 아닙니다. 그리고 주어진 행렬의 분해가 존재하지만 실수가 아니라 복소수일 수 있습니다. 현재 공부 중인 Deep Learning Book에서는 간단하게 분해 결과가 나오는 특별한 행렬들만 분해하며, 실수로 이루어진 대칭행렬은 다음과 같이 오직 실수로 이루어진 고유벡터들과 고유값들만으로 이루어진 표현식으로 분해됩니다.
\[\boldsymbol{A} = \boldsymbol{Q \Lambda Q}^\top\]
여기서 \(\boldsymbol{Q}\)는 \(\boldsymbol{A}\)의 고유벡터들로 이루어진 직교행렬이고, \(\boldsymbol{\Lambda}\)는 대각행렬입니다. 고윳값 \(\Lambda_{i, j}\)는 \(\boldsymbol{Q}\)의 열 i의 고유벡터와 연관되는데, 그 고유벡터를 \(\boldsymbol{Q}_{:, i}\)로 표기합니다. \(\boldsymbol{Q}\)는 직교행렬이므로, \(\boldsymbol{A}\)는 공간을 \(\boldsymbol{v}^{(i)}\) 방향으로 \(\lambda_i\)만큼 비례한 것이라고 할 수 있습니다. 아래 그림은 그러한 공간 비례의 예시를 보여줍니다.
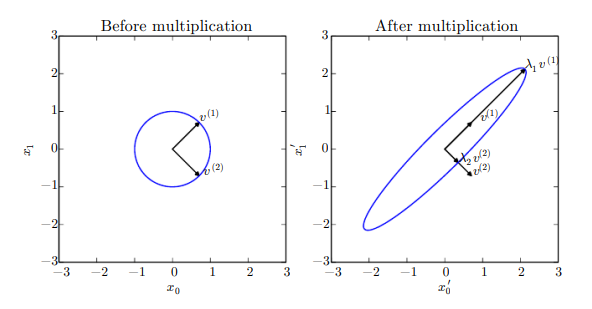
임의의 실수로 구성된 대칭행렬 \(\boldsymbol{A}\)에는 적어도 하나의 고윳값 분해가 존재합니다. 그러나 그 고윳값 분해가 유일하다는 보장은 없습니다. 둘 이상의 고유벡터들이 동일한 고윳값을 가지고 있다면, 해당 생성공간에 놓인 임의의 직교벡터들 역시 그러한 고윳값을 가진 고유벡터들이며, 그 고유벡터들도 동등하게 \(\boldsymbol{Q}\)를 선택할 수 있습니다. 관례상 \(\boldsymbol{\Lambda}\)의 성분들을 내림차순으로 정렬해서 나열합니다. 이러한 관례에서, 주어진 고윳값 분해는 오직 모든 고윳값이 유일할 때만 유일합니다.
행렬의 고윳값 분해는 행렬에 관한 여러 유용한 사실들을 말해 줍니다. 만약 고윳값 중 하나라도 0이라면, 그리고 오직 그럴 때에만 행렬은 특이행렬(singular matrix)입니다. 실수로 구성된 대칭행렬의 고윳값 분해는 \(f(\boldsymbol{x}) = \boldsymbol{x}^\top \boldsymbol{Ax}\) 형태의 이차식을 \(\left \| x \right \|_2 = 1\)이라는 제약에 따라 최적화하는 데에도 활용할 수 있습니다. \(\boldsymbol{x}\)가 \(\boldsymbol{A}\)의 한 고유벡터와 같으면 \(f\)는 해당 고윳값이 됩니다. 제약 영역 내에서 \(f\)의 최댓값을 최대 고윳값이고, 최솟값은 최소 고윳값입니다.
모든 고윳값이 양수인 행렬을 양의 정부호(positive definite) 행렬이라고 부릅니다. 그리고 모든 고윳값이 양수 또는 0인 행렬을 양의 준정부호(positive semidefinite) 행렬이라고 부릅니다. 이와 비슷하게, 모든 고윳값이 음수인 행렬은 음의 정부호(negative definite) 행렬, 모든 고윳값이 음수 또는 0인 행렬을 음의 준정부호(negative semidefinite) 행렬이라고 부릅니다. 양의 준정부호 행렬은 \(\forall\boldsymbol{x}, \boldsymbol{x}^\top \boldsymbol{Ax} \geq\)를 보장한다는 점에서 흥미롭습니다. 양의 정부호 행렬은 이외에도 \(\boldsymbol{x}^\top \boldsymbol{Ax} = \boldsymbol{0} \Rightarrow \boldsymbol{x} = \boldsymbol{0}\)도 보장합니다.
'ML & DL > Study' 카테고리의 다른 글
| Integer Quantization for Deep Learning Inference 리뷰 (0) | 2024.02.07 |
|---|---|
| [선형대수] 특잇값 분해와 유사역행렬 (0) | 2022.05.14 |
| [선형대수] Norm (노름) (0) | 2022.05.13 |
| [선형대수] 일차종속과 생성공간 (0) | 2022.05.12 |
| AutoEncoder (3) : AE, DAE (0) | 2021.02.15 |

댓글