References
- Ch4, The Art of Writing Efficient Program
Contents
- Memory Architecture
- Measuring Memory Access Speed
- Optimizing Memory Performance
포스팅에서 사용된 모든 코드는 link에서 확인할 수 있다.
CPU 다음으로 메모리가 전체 프로그램의 성능을 제한하는 경우가 많다. 이번 포스팅에서는 현대 메모리의 아키텍처, 약점, 그리고 이러한 약점을 해결하거나 최소한 숨기는 방법에 대해 살펴본다. 많은 프로그램에서 성능은 프로그래머가 하드웨어의 기능을 활용하여 메모리 성능을 얼마나 향상하는지에 전적으로 달려있다.
Superscalar
Instruction-Level Parallelism (ILP)
References Ch3, The Art of Writing Efficient Program Contents CPU Architecture Internal concurrency of the CPUs for optimum performance (Super Scalar, ILP) Visualizing ILP CPU Architecture 효율적인 프로그램은 사용 가능한 리소스를 낭비
junstar92.tistory.com
CPU는 상당히 많은 계산을 병렬로 처리할 수 있다는 것을 위의 포스팅을 통해서 살펴볼 수 있었다. 아래의 연산을 살펴보자.
for (size_t i = 0; i < N; ++i) {
a1 += p1[i] + p2[i];
a2 += p1[i] * p2[i];
a3 += p1[i] << 2;
a4 += p2[i] - p1[i];
a5 += (p2[i] << 1)*p2[i];
a6 += (p2[i] - 3)*p1[i];
}위 연산에서는 두 개의 입력만 사용된다. 그렇다면 아래처럼 8개의 입력을 사용하여 동일한 연산을 수행하는 경우에는 어떨까?
for (size_t i = 0; i < N; ++i) {
a1 += p1[i] + p2[i];
a2 += p3[i] * p4[i];
a3 += p5[i] << 2;
a4 += p5[i] - p6[i];
a5 += (p8[i] << 1) * p2[i];
a6 += (p7[i] - 3) * p1[i];
}연산 코드 자체는 이전과 동일하지만, 이제 한 반복에서 입력이 2개가 아닌 8개로 증가했다. 이렇게 작성한 벤치마크를 통해 성능을 비교해보면 그 영향이 어느 정도 존재한다는 것을 볼 수 있다.

즉, 메모리에 더 많은 데이터에 액세스할 때 연산이 다소 지연된다는 것을 확인할 수 있다.
입력 및 출력에 대한 더 많은 변수를 추가하면 성능에 영향을 미칠 수 있는 또 다른 이유가 있다는 점에 유의해야 한다. CPU에서 연산을 위해 필요한 레지스터의 수가 부족할 수 있다. 실제 많은 프로그램에서 이는 중요한 관심사가 될 수 있지만, 위의 예제의 경우는 CPU의 모든 레지스터를 사용할만큼 복잡하지 않으므로 해당되지는 않는다.
분명히 더 많은 메모리에 액세스하면 속도가 느려지는 것으로 보인다. 단순히 바라봤을 때, 이는 메모리 속도가 CPU 속도를 따라갈 수 없기 때문이다. 이러한 속도의 차이를 측정하는 방법에는 여러 방법이 있다. 가장 간단한 방법은 CPU 사양을 살펴보는 것이다. 요즘 CPU는 3GHz~4GHz 사이의 주파수 클럭에서 동작하며, 이는 한 사이클에 0.3 나노초라는 것을 의미한다. 반면, 메모리는 훨씬 느리다. 예를 들어, DDR4 메모리의 클럭은 400MHz 정도에서 동작한다. 사양을 보면 3200MHz 정도로 큰 값도 찾을 수 있지만 이는 클럭이 아닌 데이터 속도를 의미한다. 이를 메모리 속도와 유사한 값으로 변환하려면 CAS Latency 또는 CL로 알려져 있는 Column Access Strobe Latency를 고려해야 한다. 이는 대략적으로 RAM이 데이터 요청을 수신하고, 처리하고, 값을 반환하는데 걸리는 사이클 수이다. 모든 상황에서 만족하는 메모리 속도의 정의는 없지만, data rate가 3.2GHz이고 CAS Latency가 15인 DDR4 모듈의 메모리 속도는 액세스 당 107MHz, 즉, 9.4나노초로 근사될 수 있다.
어쨋듯, CPU는 메모리가 입력값을 로드하거나 결과를 저장할 수 있는 것보다 더 많은 작업을 수행할 수 있다. 모든 프로그램은 어떠한 방식으로든 메모리를 사용해야만 하며, 메모리에 액세스하는 방법에 대한 세부 사항은 성능에 상당한 영향을 미치며 때로는 성능을 제한할 수 있다. 이 세부 사항은 매우 중요하며, 이에 대한 영향은 미미한 것부터 프로그램의 병목까지 다양할 수 있다. 따라서, 최상의 성능을 위한 코드를 작성하려면 다양한 조건에서 메모리가 프로그램의 성능에 어떻게 영향을 미치는지, 그리고 그 이유가 무엇인지 이해해야 한다.
Memory Access Speed
메모리에 있는 데이터에 비해 이미 레지스터에 데이터가 로드되어 있다면 CPU가 훨씬 더 빠르게 동작할 수 있다. 프로세서와 메모리 속도의 사양으로부터 최소한 10배 정도의 차이가 있음을 알 수 있다. 그러나 직접적으로 성능을 측정하지 않고 검증하지 않고는 이러한 성능에 대해 추측이나 가정을 하지 않는 것이 좋다. 물론 아키텍처에 대한 사전 지식을 기반으로 할 수 있는 가정이 유용하지 않다는 의미는 아니다. 이러한 가정은 실험과 올바른 측정에 도움이 되로 수 있지만, 잘못된 가정은 오류로 이어질 수 있다는 사실을 유의해야 한다.
메모리 액세스 속도를 측정하는 것은 단순하다. 단지 메모리를 읽는 시간을 측정하기만 하면 된다.
volatile int* p = new int;
*p = 42;
for (auto _ : state) {
benchmark::DoNotOptimize(*p);
}
delete p;위의 벤치마크 코드는 메모리를 읽는 속도를 측정한다. 원치 않는 컴파일러 최적화로 인해 0초로 측정될 수 있기 때문에 정상적으로 코드가 수행되도록 읽을 메모리를 volatile로 선언하고 원치 않는 최적화가 발생하지 않도록 한다. 그래도 위 결과는 0초로 측정될 수 있는데, 이는 벤치마크 자체 결함이며 읽기 속도가 1나노초보다 빠르기 때문에 발생하는 것이다. 따라서, 측정을 제대로 하려면 한 번의 반복에서 한 번의 읽기가 아닌 여러 번 읽기를 수행하도록 하여 충분한 시간이 측정되도록 해야 한다. 사용할 벤치마크에서는 각 반복에서 32번의 읽기를 수행하도록 한다.
volatile int* p = new int;
*p = 42;
for (auto _ : state) {
benchmark::DoNotOptimize(*p);
... repeat 32 times ...
benchmark::DoNotOptimize(*p);
}
state.SetItemsProcessed(32*state.iterations());
delete p;for 루프를 통해 32번 반복하도록 할 수도 있지만, 해당 루프에 의한 오버헤드는 측정되면 안되므로 수작업으로 추가해야 한다. 사용된 전체 벤치마크 코드는 아래와 같다.
#define REPEAT2(x) x x
#define REPEAT4(x) REPEAT2(x) REPEAT2(x)
#define REPEAT8(x) REPEAT4(x) REPEAT4(x)
#define REPEAT16(x) REPEAT8(x) REPEAT8(x)
#define REPEAT32(x) REPEAT16(x) REPEAT16(x)
#define REPEAT(x) REPEAT32(x)
template <class Word>
void BM_read_rand(benchmark::State& state) {
volatile Word* const p = new Word;
::memset((void*)p, 0xab, sizeof(Word));
for (auto _ : state) {
REPEAT(benchmark::DoNotOptimize(*p);)
}
delete p;
state.SetBytesProcessed(32*sizeof(Word)*state.iterations());
state.SetItemsProcessed(32*state.iterations());
}
BENCHMARK_TEMPLATE1(BM_read_rand, unsigned int);
BENCHMARK_TEMPLATE1(BM_read_rand, unsigned long);위 벤치마크 결과는 다음과 같다.

32번의 읽기에 걸리는 시간이 3.35ns로 측정되므로, 한 번의 읽기가 1나노초 이내로 수행된다는 것을 알 수 있다. 하지만, 이 결과는 메모리에 액세스하는 속도가 느리다는 우리의 예상과 일치하지 않는다. 성능의 병목을 일으키는 원인에 대한 가능성이 틀렸을 가능성이 있거나 메모리 속도가 아닌 다른 것을 측정했을 수도 있다.
Memory Architecture
메모리 성능을 올바르게 측정하는 방법을 이해하려면 프로세서의 메모리 아키텍처에 대해 이해해야 한다. 메모리 시스템의 가장 중요한 특징은 계층을 이루고 있다는 것이다. CPU는 메인 메모리에 직접 액세스하지 않고 캐시 계층을 통해 액세스한다. 메모리 계층 구조는 아래와 같다. RAM은 메인 메모리(DRAM)를 나타낸다.

위 그림을 보다시피 CPU는 메인 메모리에 직접 액세스하지 않고 여러 레벨의 캐시 계층을 통해 액세스한다. 캐시도 메모리이지만 데이터를 저장하기 위해 SRAM이라는 기술을 사용한다. DRAM과 SRAM의 주요한 차이점은 SRAM의 액세스 속도가 훨씬 빠르지만 DRAM보다 더 많은 전력을 소비한다는 것이다. 메모리 계층 구조에서 CPU에 가까워질수록 메모리 액세스 속도는 증가한다. Level-1 (L1) 캐시는 CPU 레지스터와 액세스 속도가 거의 동일하지만 너무 많은 전력을 소모한다. L1 캐시 메모리는 수 킬로바이트에 불과하며, 일반적으로 CPU 코어 당 32KB인 경우가 많다. 그 다음 레벨의 캐시인 L2 캐시는 L1보다 용량은 더 크지만, 더 느리다. 세 번째 캐시인 L3 캐시는 훨씬 더 크지만 훨씬 더 느리며, 일반적으로 CPU의 코어 간에 공유된다. 계층 구조의 마지막은 메인 메모리이다.
M1 Mac의 경우 L1 캐시의 크기가 64KB이다.
CPU가 처음 메인 메모리로부터 데이터 값을 읽으면 그 값은 모든 캐시 레벨에 전파되고, 그 사본은 캐시에 남는다. CPU가 동일한 값을 다시 읽으면 동일한 값의 복사본이 이미 캐시에 존재하므로 메인 메모리로부터 값을 가져올 때까지 기다릴 필요가 없다.
모든 데이터는 처음 액세스할 때 캐시에 로드되며, 그 이후에는 CPU가 캐시에 액세스하기만 하면 된다. 그러나 현재 캐시에 존재하지 않는 값에 액세스하려고 시도하고 캐시는 이미 가득찬 경우에는 새 값을 위한 공간을 확보하기 위해 캐시에서 무언가를 제거해야 한다. 이 프로세서는 전적으로 하드웨어에 의해 제어된다. 하드웨어는 비교적 최근에 액세스한 값을 기반으로 다시 필요할 가능성이 낮은 값을 제거하는 휴리스틱한 방법을 사용한다. L1부터 이러한 작업이 수행되며, 다음 레벨의 캐시에서도 동일한 방식이 적용된다. 즉, 데이터가 캐시에 있다면 해당 캐시에서 값을 가져오게 되고, 그렇지 않으면 다음 레벨의 캐시로부터 값을 가져온다. L3 캐시의 경우에는 메인 메모리로부터 가져와야 하는 것이다.
이제 처음 측정한 메모리 읽기 속도가 왜 빠른지 알 수 있다. 동일한 값만 수만 번 반복해서 읽었기 때문에 초기 읽기 비용은 무시된다. 즉, 측정된 평균 메모리 읽기 시간은 L1 캐시로부터 읽은 시간이다. L1 캐시는 실제로 상당히 빠르다. 이러한 이유로 메모리 성능을 올바르게 측정하는 방법을 알아야 프로그램에 적용할 수 있다.
Measuring Memory and Cache Speeds
지금까지 살펴본 내용을 토대로 보다 적절한 벤치마크를 작성할 수 있다. 캐시의 크기가 결과에 상당한 영향을 미칠 것으로 예상할 수 있으므로 수 킬로바이트(32KB L1 cache)부터 수십 메가바이트 이상(L3 캐시 크기는 다양하지만 일반적으로 8MB~12MB)까지 다양한 크기의 데이터에 액세스하도록 해야 한다. 대용량 데이터의 경우, 메모리 시스템이 캐시에서 기존 데이터를 제거해야 하기 때문에 성능은 해당 예측이 얼마나 잘 동작하는지에 따라 달라질 수 있다. 조금 더 일반적으로 말하면, 메모리 액세스 패턴에 따라 성능이 달라질 수 있다고 할 수 있다. 메모리 특정 범위를 복사하는 것과 같은 순차적 액세스는 동일한 메모리 범위를 무작위로 액세스하는 것과 상당히 다르게 수행될 수 있다. 또한, 결과는 메모리 액세스의 세분성(granularity)에 따라 달라질 수 있다 (32비트 액세스 vs 64비트 액세스).
The Speed of Random Memory Access
무작위 순서로 메모리에 액세스하는 벤치마크 구현은 다음과 같다. 각각 read와 write에 대한 벤치마크이다.
template <class Word>
void BM_read_rand(benchmark::State& state) {
void* memory;
const size_t size = state.range(0);
if (::posix_memalign(&memory, 64, size) != 0) abort();
void* const end = static_cast<char*>(memory) + size;
volatile Word* const p0 = static_cast<Word*>(memory);
Word* const p1 = static_cast<Word*>(end);
const size_t N = size/sizeof(Word);
std::vector<int> v_index(N);
for (size_t i = 0; i < N; ++i) v_index[i] = i;
std::random_shuffle(v_index.begin(), v_index.end());
int* const index = v_index.data();
int* const i1 = index + N;
for (auto _ : state) {
for (const int* ind = index; ind < i1; ) {
REPEAT(benchmark::DoNotOptimize(*(p0 + *ind++));)
}
benchmark::ClobberMemory();
}
::free(memory);
state.SetBytesProcessed(size*state.iterations());
state.SetItemsProcessed((p1 - p0)*state.iterations());
char buf[1024];
snprintf(buf, sizeof(buf), "%lu", size);
state.SetLabel(buf);
}
template <class Word>
void BM_write_rand(benchmark::State& state) {
void* memory;
const size_t size = state.range(0);
if (::posix_memalign(&memory, 64, size) != 0) abort();
void* const end = static_cast<char*>(memory) + size;
volatile Word* const p0 = static_cast<Word*>(memory);
Word* const p1 = static_cast<Word*>(end);
Word fill1; ::memset(&fill1, 0xab, sizeof(fill1));
Word fill = {}; //fill1;
const size_t N = size/sizeof(Word);
std::vector<int> v_index(N);
for (size_t i = 0; i < N; ++i) v_index[i] = i;
std::random_shuffle(v_index.begin(), v_index.end());
int* const index = v_index.data();
int* const i1 = index + N;
for (auto _ : state) {
for (const int* ind = index; ind < i1; ) {
REPEAT(*(p0 + *ind++) = fill;)
}
benchmark::ClobberMemory();
}
benchmark::DoNotOptimize(fill);
::free(memory);
state.SetBytesProcessed(size*state.iterations());
state.SetItemsProcessed((p1 - p0)*state.iterations());
char buf[1024];
snprintf(buf, sizeof(buf), "%lu", size);
state.SetLabel(buf);
}랜덤 인덱스로 메모리에 액세스하려고 for 루프 내에서 rand()를 사용하여 랜덤 인덱스를 생성하는 방식을 사용하면 rand() 호출 비용을 측정에 포함되므로 잘못된 결과를 얻을 수 있다. 정확한 결과를 얻으려면 무작위 랜덤 인덱스를 미리 계산하여 다른 배열에 저장한 뒤, 이를 사용하는 것이다. 물론, 인덱스 값과 인덱싱된 데이터를 모두 읽으므로 실제 측정된 결과는 두 번의 read (또는 read와 write)의 비용이라는 것이다.
위 코드에서는 STL의 random_shuffle()을 사용하여 무작위 순서의 인덱스를 생성한다. 난수를 사용해도 되지만, 일부 인덱스는 두 번 이상 나타나거나 한 번도 나타나지 않을 수도 있다. 다만 그렇다고 결과에 큰 영향을 미치지는 않는다. 메모리에 쓰는 값은 크게 중요하지 않지만, 코드가 메모리에 0을 많이 쓴다는 것을 알아낼 수 있으면 컴파일러가 때때로 특별한 최적화를 수행할 수 있으므로 피하는 것도 좋다.
unsigned int와 unsigned long에 대한 random read와 random write 벤치마크 결과는 각각 다음과 같다. 아래 결과는 M1 Mac에서 측정한 결과이다.


먼저 read access 속도를 살펴보자. 아래 그래프는 순서대로 words per seconds (unit: G)와 seconds per a word (unit: ns)에 대한 결과를 나타낸다.


그래프에서 확인할 수 있는 몇 가지 특징이 있다.
먼저 예상한대로 속도가 일정하지 않다. 하나의 32비트 정수 또는 64비트 정수를 읽는데 걸리는 시간은 약 0.2나노초에서 약 5.5나노초까지 다양하다. 적은 양의 데이터를 읽을 때가 많은 양을 읽을 때보다 훨씬 빠르다. 이 그래프에서 캐시 크기를 짐작할 수 있는데, M1 Mac의 경우 L1 캐시의 크기가 64KB이다. 즉, 데이터의 범위가 64KB 이내인 경우에는 L1 캐시의 속도로 읽고 있다는 것을 알 수 있다. 데이터가 64KB를 초과하는 순간부터 속도가 떨어지기 시작하는 모습을 보여준다. 그러면 이제 L2 캐시(4096KB) 크기에는 맞으면 L2 캐시 크기에 맞을 때까지는 어느 정도 속도를 유지하다가 L2 캐시 크기보다 더 초과하게 되면 속도가 더 떨어진다. 데이터가 캐시 크기에 맞는 한 어느 정도 캐시의 이점을 활용한다. 하지만 데이터의 크기가 캐시보다 수 배 이상으로 초과하면 액세스 시간은 전적으로 메모리에서 데이터를 검색하는데 걸리는 시간에 의해서 결정된다.
두 번째는 결과 값 자체가 흥미롭다는 것이다. 데이터 크기가 1024MB일 때, 즉, 데이터를 캐시가 아닌 메모리에서 하나의 정수를 읽는데 약 5나노초가 걸린다. 이는 매우 긴 시간이며, CPU는 나노초 내에 여러 작업들을 수행할 수 있으므로 CPU는 이 시간에 수십 개의 산술 연산을 수행할 수 있다. 일반적으로 하나의 값에 대해 수십 개의 연산을 수행하는 프로그램은 거의 없으므로, 메모리 액세스 속도를 높일 수 있는 방법을 찾지 못하면 CPU의 활용률이 낮을 가능성이 높다.
마지막으로 초당 워드를 읽는 속도는 워드의 크기에 의존하지 않는다는 것을 알 수 있다. 즉, 32비트보다 64비트를 사용하면 동일한 시간에 2배 더 많은 데이터를 읽을 수 있다는 것이다. SIMD 명령어를 사용하면 128비트 크기의 데이터를 사용하여 동일한 시간에 32비트보다 4배 더 많은 데이터를 읽을 수도 있을 것이다. 속도가 워드 크기에 의존하지 않는다는 사실에는 또 다른 의미가 있다. 이는 읽기 속도가 bandwidth가 아닌 latency에 의해 제한된다는 것을 의미한다. Latency는 데이터 요청이 발행된 시간과 검색되는 시간 사이의 지연 시간이다.
메모리 쓰기 속도에 대한 동일한 결과의 그래프는 다음과 같다.


Random read 속도와 random write 속도는 유사하지만 이는 하드웨어에 따라 다르며, 보통 read가 조금 더 빠르다. 내가 측정한 결과도 read가 조금 더 빨랐다.
위 결과를 통해, 크기가 작은 데이터(여기서는 64KB 이하)에 반복적으로 무작위 액세스하는 것은 크게 걱정할 필요가 없다. 물론 여기서는 반복이 핵심이다. 모든 메모리 위치에 대한 첫 번째 액세스는 액세스하는 메모리 크기에 관계없이 메인 메모리로부터 액세스하게 된다. 반면, 큰 메모리의 데이터에 액세스하는 경우에는 무작위 액세스가 문제가 될 수 있다고 결론 내릴 수 있다.
정리하면 다음과 같다.
무작위로 데이터를 액세스하게 되면, 모든 메모리 액세스가 사실상 새로운 액세스가 된다. 읽으려는 전체 배열은 들어갈 수 있는 가장 작은 캐시에 로드되며, 읽기 및 쓰기 작업은 해당 캐시의 무작위 위치에 액세스하게 된다. 배열 크기가 캐시에 맞지 않으면 메모리의 다른 위치에 무작위로 액세스하려고 시도하며 수 나노초의 latency가 발생하게 된다.
The Speed of Sequential Memory Access
프로그램에서 무작위 액세스가 자주 발생하지만, 종종 첫 번째 요소부터 마지막 요소까지 처리해야 하는 큰 배열이 있을 수 있다. 이때 배열을 순차적으로 처음부터 끝까지 읽으면 메모리 주소가 단조롭게 증가하여 메모리에 순차적으로 액세스하게 된다.
순차적으로 배열을 읽는 벤치마크는 아래와 같이 간단하게 작성할 수 있다.
template <class Word>
void BM_read_seq(benchmark::State& state) {
void* memory;
const size_t size = state.range(0);
if (size/sizeof(Word) < 32) abort();
if (::posix_memalign(&memory, 64, size) != 0) abort();
void* const end = static_cast<char*>(memory) + size;
volatile Word* const p0 = static_cast<Word*>(memory);
Word* const p1 = static_cast<Word*>(end);
for (auto _ : state) {
for (volatile Word* p = p0; p != p1; ) {
REPEAT(benchmark::DoNotOptimize(*p++);)
}
benchmark::ClobberMemory();
}
::free(memory);
state.SetBytesProcessed(size*state.iterations());
state.SetItemsProcessed((p1 - p0)*state.iterations());
char buf[1024];
snprintf(buf, sizeof(buf), "%lu", size);
state.SetLabel(buf);
}
template <class Word>
void BM_write_seq(benchmark::State& state) {
void* memory;
const size_t size = state.range(0);
if (::posix_memalign(&memory, 64, size) != 0) abort();
void* const end = static_cast<char*>(memory) + size;
volatile Word* const p0 = static_cast<Word*>(memory);
Word* const p1 = static_cast<Word*>(end);
Word fill1; ::memset(&fill1, 0xab, sizeof(fill1));
Word fill = fill1;
for (auto _ : state) {
for (volatile Word* p = p0; p != p1; ) {
REPEAT(*p++ = fill;)
}
benchmark::ClobberMemory();
}
benchmark::DoNotOptimize(fill);
::free(memory);
state.SetBytesProcessed(size*state.iterations());
state.SetItemsProcessed((p1 - p0)*state.iterations());
char buf[1024];
snprintf(buf, sizeof(buf), "%lu", size);
state.SetLabel(buf);
}
#define ARGS \
->RangeMultiplier(2)->Range(1<<10, 1<<30)
BENCHMARK_TEMPLATE1(BM_write_seq, unsigned int) ARGS;
BENCHMARK_TEMPLATE1(BM_write_seq, unsigned long) ARGS;
unsigned int 타입과 unsigned long 타입에 대한 각 벤치마크 실행 결과는 다음과 같다.


순차적 쓰기 액세스 결과에 대한 그래프(워드 하나를 쓰는데 걸리는 시간)는 다음과 같다.
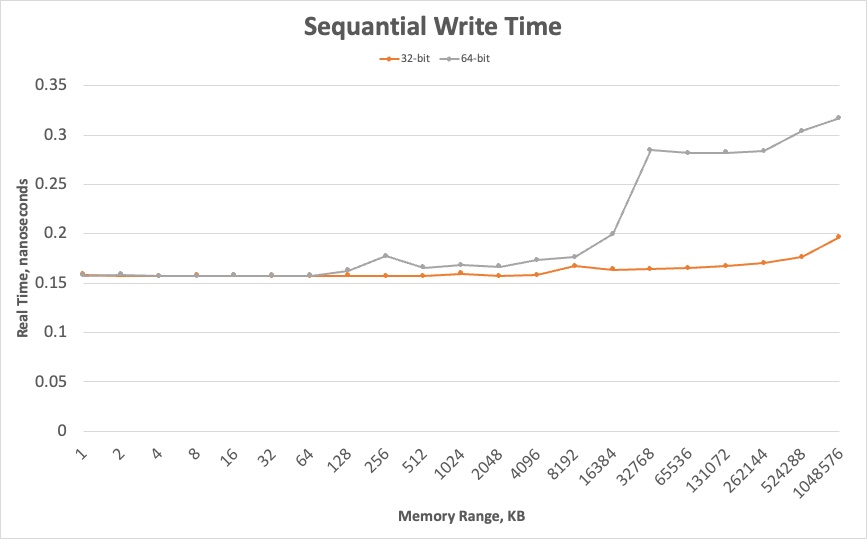
그래프의 전반적인 형태는 무작위 액세스와 동일하지만, 차이점은 존재한다. 주목할 부분은 바로 세로 축의 크기이다. 무작위로 액세스할 때보다 그 크기가 훨씬 작다. 1048MB의 데이터에서도 64bit 정수 하나를 쓰는데 걸리는 시간이 약 0.3 나노초로 측정된다.
두 번째로 주목할 부분은 각 워드 크기에 대한 그래프가 일치하지 않다는 것이다. 일치하지 않는 정도의 차이는 하드웨어에 따라 다르다. 32비트 데이터와 64비트 데이터에 대한 순차적 쓰기 시간은 L1 캐시 크기에 데이터 크기가 맞는 경우에는 동일하지만, L1 캐시 크기를 벗어나는 순간 달라진다. 일정 크기 이전까지는 64비트 정수를 쓰는데 걸리는 시간이 32비트 정수를 쓰는데 걸리는 시간의 두 배가 되지 않지만, 일정 크기 이상에서는 두 배가 된 다는 것을 알 수 있다. 즉, 이제 성능 제한은 초당 얼마나 많은 워드를 쓸 수 있는지가 아닌 얼마나 많은 바이트를 쓸 수 있는지이다. 이는 이제 속도가 latency가 아닌 bandwidth에 의해 제한됨을 의미한다. 순차적 메모리 액세스에서는 버스가 전송할 수 있는 속도만큼 빠르게 메모리에 푸시하며, 이 비트를 32비트로 그룹화하든지 64비트 그룹화하든지는 상관없다.
마지막으로 주목할 부분은 이전의 무작위 액세스에서는 캐시 크기를 초과할 때마다 그래프가 가파르게 꺽였지만, 순차적 액세스에서는 그렇지 않다는 것이다.
Memory Performance Optimizations in Hardware
무작위 액세스와 순차적 액세스 벤치마크 코드의 차이는 메모리 액세스 순서를 변경하는 것 외에는 없다. 따라서, 벤치마크 결과를 종합하여 생각해보면, 하드웨어 자체에서 사용하는 일종의 latency-hiding 기법이 있음을 추정할 수 있다. 메인 메모리로부터 무작위로 액세스할 때는 수 나노초가 걸린다. 이는 특정 주소의 데이터를 요청한 시간부터 CPU 레지스터로 전달될 때까지 걸리는 시간이며, 이는 전적으로 latency에 의해 결정된다 (요청된 바이트 크기는 중요하지 않다). 메모리에 순차적으로 액세스할 때는 하드웨어가 배열의 다음 요소 전송을 즉시 시작할 수 있다. 첫 번째 요소에 액세스하기 까지는 여전히 수 나노초가 걸리지만, 그 이후에는 하드웨어가 전체 배열을 메모리에서(또는 메모리로) 스트리밍을 시작할 수 있다. 배열의 두 번째 요소의 전송은 CPU가 데이터에 대한 요청을 발행하기 전에 이미 시작된다. 따라서 latency는 더 이상 제한 요소가 아니며, bandwidth가 제한 요소가 된다.
물론 이와 같은 작업은 하드웨어가 전체 배열을 순차적으로 액세스할 것이고, 배열이 얼마나 큰지 알고 있다고 가정한다. 실제로 하드웨어는 이러한 정보를 전혀 모르지만, CPU의 조건부 명령과 마찬가지로 메모리 시스템에는 학습하여 추측하는 회로가 있다. 여기에서는 prefetch(프리패치)라는 하드웨어 기법이 사용된다. 메모리 컨트롤러는 CPU가 여러 주소를 순차적으로 액세스한 것을 알게 되면, 이러한 패턴이 계속될 것이라고 가정하고 데이터를 L1 캐시로 전송하거나 캐시의 공간을 비워서 다음 메모리 위치에 대한 액세스를 미리 준비한다. 이 기법을 통해 이상적으로 CPU가 각 배열 요소를 필요로 할 때 이미 이 값들이 L1 캐시에 있으므로 CPU는 항상 L1 캐시 속도로 메모리에 액세스할 수 있다. 실제 프로그램에서 이러한 이상적인 경우를 만족하는지 여부는 인접한 요소에 액세스하는 사이에 CPU가 수행하는 작업의 양에 따라 달라진다. 이전의 벤치마크에서는 CPU가 거의 아무런 작업도 하지 않기 때문에 프리패치가 뒤처지게 된다.
프리패치는 메모리 액세스 방법에 대한 예측이나 사전 지식을 기반으로 하지 않는다. 대신 메모리 액세스 패턴을 감지하려고 시도한다. 따라서, 프리패치의 효율성은 얼마나 효과적으로 패턴을 파악하고 다음 액세스 위치를 추측할 수 있는지에 따라 결정된다.
프리패치 감지 패턴의 한계에 대해서 많은 정보가 있지만 대다수는 이제 적용되지 않는 내용들이다. 따라서, 프리패치 측면에서 어떤 패턴이 효율적이고 효율적이지 않은지 정확하게 설명하는 것보다는 궁극적으로 특정 알고리즘에 특정 메모리 액세스 패턴이 필요하고 프리패치가 이를 처리할 수 있는지 확인하는 벤치마크 코드를 통해 평가하고 측정하는 것이 가장 유용할 수 있다.
일반적으로 메모리를 증가하는 순서로 액세스하는 것과 감소하는 순서로 액세스하는 것은 모두 프리패치 측면에서 효과적이라고 할 수 있다. 다만, 방향을 바꾸면 프리패치가 새로운 패턴을 학습할 때까지 약간의 패널티는 있을 수 있다. 스트라이드(stride)를 사용하여 일정한 간격으로 떨어진 요소마다 액세스하는 것도 효과적으로 감지되고 예측된다. 여러 개의 스트라이드, 예를 들어, 3번째 및 7번째 요소마다 액세스하는 것과 같은 패턴도 감지할 수 있지만 이는 하드웨어마다 다르다.
하드웨어가 성능을 최적화할 수 있는 또 다른 기법은 pipelining 또는 hardware loop unrolling이다. 파이프라이닝은 메모리 액세스 latency를 숨기는데 사용될 수 있다. 아래 얘제 코드를 살펴보자.
for (size_t i = 0; i < N; ++i) {
b[i] = func(a[i]);
}매 반복마다 배열로부터 a[i] 값을 읽고, 연산을 수행하고, 결과를 다른 배열의 b[i]에 저장한다. 읽고 쓰는데 시간이 걸리므로, 우리는 이 루프의 타임라인은 아래와 같을 것이라고 예상할 수 있다.

위와 같은 일련의 연산에서 CPU는 메모리 연산이 완료될 때까지 기다리게 된다. 대신, 하드웨어는 명령어 스트림을 미리 읽어서 서로 의존하지 않는 명령어 시퀀스를 아래와 같이 오버랩할 수 있다.

파이프라이닝은 메모리 액세스의 latency를 숨길 수 있지만 명백히 한계는 존재한다. 만약 하나의 값을 읽는데 7나노초가 걸리고, 백만 개의 값을 읽어야 한다면 7ms가 걸리게 된다. 이 시간을 피할 방법은 없다. 파이프라이닝은 연산과 메모리 작업을 중첩하여 이상적으로 모든 계산을 7ms 동안 완료할 수 있다. 프리패치는 어떤 값을 필요로 하기 전에 다음 값을 읽는 것을 시작할 수 있다. 따라서, 평균 읽기 시간을 줄일 수는 있다. 단, 다음 읽을 값을 정확하게 추측하는 경우에만 가능하다.
Optimizing Memory Performance
대부분의 프로그램에서 처리하는 데이터 크기는 L1 캐시의 크기보다 훨씬 크다. 따라서, 프로그램에서 메모리 성능을 향상시켜야 더 좋은 성능의 프로그램을 구현할 수 있다.
Memory-Efficient Data Structures
일반적으로 데이터 구조는 프로그래머가 데이터 성능과 관련하여 내릴 수 있는 가장 중요한 결정 중 하나이다. 프로그램에서 무엇을 할 수 있는지 무엇을 할 수 없는지 이해하는 것이 중요하며, 위에서 살펴본 메모리 성능은 실제 성능이며 회피할 수 없는 부분이다. 하지만, 사용하는 메모리 범위의 크기 정도는 어느 정도 선택할 수 있으며, 이를 잘 선택하여 그나마 빠른 액세스가 가능하도록 해야 한다. 예를 들어, 순차적으로 저장하고 처리해야 하는 백 만개의 64비트 정수가 있다고 가정해보자. 이 값을 배열에 저장하려면, 배열의 크기는 8MB가 될 것이다. 측정에 따르면 이 경우의 액세스 속도는 약 0.18 나노초이다.
배열 대신 리스트를 사용하여 동일한 값을 저장할 수도 있다. 리스트는 노드들의 집합이며, 각 노드에는 값과 다음 노드 및 이전 노드를 가리키는 두 개의 포인터를 가진다. 따라서, 전체 리스트는 24MB 메모리를 사용하게 될 것이다. 또한, 각 노드는 별도의 new 연산자 호출로 할당되므로 서로 다른 노드들이 전혀 다른 주소에 있을 가능성이 높다. 따라서, 리스트를 탐색할 때 액세스하는 주소에 어떠한 패턴도 없이 무작위로 액세스하게 되는 것과 같을 것이며, 액세스 속도는 느릴 것이다.
배열(std::vector)와 리스트(std::list)에 대한 벤치마크를 통해 성능을 비교해보자.
template <class Word>
void BM_read_vector(benchmark::State& state) {
const size_t size = state.range(0);
std::vector<Word> c(size);
{
Word x = {};
for (auto it = c.begin(), it0 = c.end(); it != it0; ++it) *it = ++x;
}
for (auto _ : state) {
for (auto it = c.begin(), it0 = c.end(); it != it0; ) {
REPEAT(benchmark::DoNotOptimize(*it++);)
}
benchmark::ClobberMemory();
}
state.SetBytesProcessed(size*sizeof(Word)*state.iterations());
state.SetItemsProcessed(size*state.iterations());
char buf[1024];
snprintf(buf, sizeof(buf), "%lu", size);
state.SetLabel(buf);
}
template <class Word>
void BM_write_vector(benchmark::State& state) {
const size_t size = state.range(0);
std::vector<Word> c(size);
Word x = {};
for (auto _ : state) {
for (auto it = c.begin(), it0 = c.end(); it != it0; ) {
REPEAT(benchmark::DoNotOptimize(*it++ = x);)
}
benchmark::ClobberMemory();
}
state.SetBytesProcessed(size*sizeof(Word)*state.iterations());
state.SetItemsProcessed(size*state.iterations());
char buf[1024];
snprintf(buf, sizeof(buf), "%lu", size);
state.SetLabel(buf);
}
template <class Word>
void BM_read_list(benchmark::State& state) {
const size_t size = state.range(0);
std::list<Word> c;
{
Word x = {};
for (size_t i = 0; i < size; ++i) c.push_back(x++);
}
for (auto _ : state) {
for (auto it = c.begin(), it0 = c.end(); it != it0; ) {
REPEAT(benchmark::DoNotOptimize(*it++);)
}
benchmark::ClobberMemory();
}
state.SetBytesProcessed(size*sizeof(Word)*state.iterations());
state.SetItemsProcessed(size*state.iterations());
char buf[1024];
snprintf(buf, sizeof(buf), "%lu", size);
state.SetLabel(buf);
}
template <class Word>
void BM_write_list(benchmark::State& state) {
const size_t size = state.range(0);
std::list<Word> c(size);
Word x = {};
for (auto _ : state) {
for (auto it = c.begin(), it0 = c.end(); it != it0; ) {
REPEAT(benchmark::DoNotOptimize(*it++ = x);)
}
benchmark::ClobberMemory();
}
state.SetBytesProcessed(size*sizeof(Word)*state.iterations());
state.SetItemsProcessed(size*state.iterations());
char buf[1024];
snprintf(buf, sizeof(buf), "%lu", size);
state.SetLabel(buf);
}1MB 크기의 메모리에 대한 벤치마크 결과는 다음과 같다.

보다시피 벡터의 성능이 훨씬 좋다. 그럼에도 리스트를 사용하는 경우가 있을 수 있는데, 예를 들어, 생성 당시에 얼마나 많은 데이터를 사용할 지 모르는 경우가 있다. 벡터 크기를 런타임에 키우는 것은 관련된 복사로 인해 비효율적이다. 데이터의 최종 크기를 미리 계산하는 방식으로 이 문제를 해결할 수는 있다. 또는, 입력을 크기를 계산하기 위해 전체 탐색을 한 번 하고, 값에 대한 처리를 위해 한 번 더 탐색하는 방식의 2단계 스캔이 성능이 더 좋을 수도 있다.
최종 데이터 크기를 미리 알 수 없다면 벡터의 메모리 효율성과 리스트의 동적 할당 효율성을 결합한 스마트한 데이터 구조를 사용할 수도 있다. 이를 block-allocated array(deque) 라고 한다.

이러한 데이터 구조는 일반적으로 L1 캐시 크기에 맞는 고정된 크기의 블록으로 메모리를 할당한다. 각 블록은 배열이므로 블록 내 요소들은 순차적으로 액세스된다. 블록 자체는 리스트로 구성된다. 각 블록의 첫 번째 요소에 액세스할 때는 캐시 미스가 발생할 가능성이 높지만, 순차적 액세스 패턴을 감지하면 블록의 나머지 요소들은 L1 캐시 속도로 액세스할 수 있다. C++ STL의 경우, std::deque 자료구조가 있지만, 대부분의 구현에서 별로 효율적이지 못하며 deque에 대한 순차적 액세스는 일반적으로 동일한 크기의 벡터에 대한 액세스보다 다소 느리다.
배열보다 리스트가 더 선호될 수 있는 이유 중 하나는 리스트는 어느 지점에서도 빠른 삽입이 가능하다는 것이다. 이런 기능이 필요하다면 리스트 또는 다른 node-allocated 컨테이너를 사용해야 한다. 이와 같은 경우에 가장 좋은 솔루션은 모든 요구 사항을 만족시키는 단일 데이터 구조를 사용하는 것이 아니라 다른 데이터 구조로 마이그레이션하는 것이다.
알고리즘에서 데이터 액세스 패턴이 변경되는 지점이 있는 경우, 메모리를 일부 복사하는 비용이 들더라도 해당 지점에서 복사하여 데이터 구조를 변경하는 것이 종종 유리할 때가 있다. 예를 들어, 리스트를 구성한 뒤, 더 이상 요소를 추가할 일이 없다면 이를 배열로 복사하여 순차적으로 액세스하는 것이 더 빠를 수 있다. 전체 데이터, 혹은 일부 데이터가 완전하다고 확신하는 경우에는 해당 부분만 배열로 복사하여 사용하고 나머지 부분은 여전히 변경 가능한 리스트 구조로 남겨둘 수도 있다.
결론은 일부 데이터에 많이 액세스하는 경우, 이러한 액세스 패턴을 최적으로 만드는 데이터 구조를 선택해야 한다는 것이다. 액세스 패턴이 바뀌면, 데이터 구조도 바껴야 한다. 하지만, 데이터에 액세스하는 시간이 적다면, 데이터 구조를 바꾸는 비용이 더 클 수 있다. 이 경우에는 데이터 액세스 비용이 애초에 문제가 되지 않으므로 신경쓰지는 않아도 된다.
중요한 것은 프로그램 내에서 어떠한 데이터가 비효율적으로 액세스되는지 알아내고, 이를 해결하기 위해 적절한 최적화를 적용하는 것이다.
Profiling Memory Performance
데이터 구조의 효율성은 명확하다. 예를 들어, 배열이나 벡터를 사용하는 클래스가 존재하고, 이 클래스의 인터페이스는 처음부터 끝까지 forward iterator를 통해 순차적으로 반복하여 데이터에 액세스한다면, 메모리 수준에서 최대의 효율로 액세스된다는 것을 확신할 수 있다. 알고리즘의 효율성에 대해서는 확신할 수는 없다. 예를 들어, 요소의 수가 매우 클 때, 특정 요소에 대한 linear search는 비효율적이다.
따라서, 어떤 데이터 구조가 메모리에 효율적인지 아는 것만으로는 충분하지 않으며, 프로그램이 특정 데이터셋에 대해 작업할 때 얼마나 많은 시간을 소비하는지 알아야 한다. 이는 코드가 캡슐화가 잘 되어 있다면 파악하기가 쉽다. 이런 경우에는 프로파일링 결과를 통해 함수 내부 코드가 계산에 특별히 부담을 주지는 않지만 데이터를 이동하는 함수나 코드 등을 쉽게 발견할 수 있고, 데이터에 대한 액세스를 보다 효율적으로 수정해주면 전반적인 성능이 향상될 가능성이 높다.
다만, 이런 부분들은 최적화하기 매우 쉬운 케이스에 속한다. 런타임 측면에서 여전히 비효율적이라고 생각되지만, 비효율적인 단일 함수나 코드들이 눈에 띄지 않을 수 있다. 런타임에서 시간이 많이 먹는 코드를 핫코드(hot code)라고 부르는데, 이러한 핫코드가 없지만 비효율적이라는 것이다. 핫코드가 없지만 비효율적인 경우에는 핫데이터(hot data)가 있는 경우가 매우 많다. 이런 데이터는 보통 프로그램 전체에서 액세스되는 데이터 구조이며, 이 데이터에 소비되는 누적 시간은 어마어마할 수 있지만 단일 함수나 코드로 보면 미미한 경우가 많다. 즉, 이러한 데이터 구조에 소비되는 시간은 많지만 전체 프로그램에 고르게 분포되어 있어서, 기존의 프로파일링으로는 쉽게 발견할 수 없고 단일 함수나 코드 조각을 최적화하더라도 개선이 미미하다는 것이다. 따라서, 프로그램 전반에 걸쳐서 비효율적으로 사용되는 데이터를 찾는 방법이 중요하다.
타이밍 성능 측정 도구만으로는 이러한 정보를 수집하기가 매우 어려운데, 하드웨어 이벤트 카운터를 사용하는 프로파일러를 사용하면 상당히 쉽게 수집할 수 있다. 대부분의 CPU는 메모리 액세스, 특히 캐시 히트 및 미스를 계산할 수 있다. 가장 많이 사용되는 도구 중 하나는 perf 이다.
아래와 같은 커맨드를 통해 프로파일링을 할 수 있다. 캐시 관련 카운터는 기본으로 측정되는 메트릭이 아니므로 명시적으로 지정해주어야 한다. 사용되는 메트릭은 CPU마다 다를 수 있으므로 perf list 커맨드를 통해 확인이 필요하다. 아래 커맨드는 L1 cache miss를 측정하며, dcache는 data cache를 의미한다 (instruction cache도 있음).
| $ perf stat -e cycles,instructions,L1-dcache-load-misses,L1-dcache-loads ./program |
이전에 살펴본 random read 벤치마크에 대해서 16KB로 데이터 크기를 지정하여 프로파일링한 결과는 다음과 같다. 보다시피 캐시 미스가 거의 발생하지 않는다.

메모리를 128MB로 증가시키면 캐시 미스가 더 자주 발생하게 된다는 것을 알 수 있다.
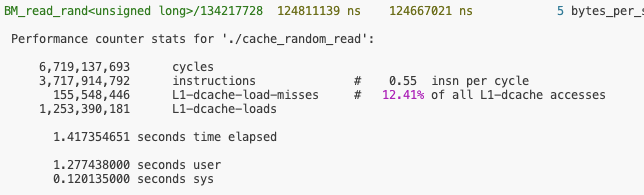
이렇게 일부 메모리 액세스가 비효율적이라는 것을 확인했으면, 이제 라인별로 살펴보면서 찾아나가면 된다. 캐시 미스 비율이 큰 코드 위치가 많이 존재할 텐데, 각 위치에서는 전체 실행 시간의 일부이지만 누적되어 나타나게 된다. 서로 다른 함수들에서 메모리에 액세스하지만, 이 메모리가 동일한 데이터 구조에서 동작하는 경우에는 데이터 구조에 문제가 있다고 판단할 수 있고 이에 대한 최적화가 필요하다.
다만, 서로 다른 데이터 구조의 기능과 성능이 각각 다르다. 따라서, 임의의 위치에 삽입을 해야 하는 경우에는 리스트를 벡터로 대체하는 방식은 사용할 수 없다. 종종 비효율적인 메모리 액세스를 요구하는 것은 데이터 구조 때문이 아닌 알고리즘 자체의 문제일 수 있다. 이런 경우에는 알고리즘 자체를 다시 생각해봐야 하며, 알고리즘을 변경해야 할 수도 있다. 알고리즘에 대한 내용은 여기서 따로 다루지는 않는다.
'프로그래밍 > Optimizations' 카테고리의 다른 글
| Lock-Based, Lock-Free, Wait-Free Program (0) | 2024.02.02 |
|---|---|
| Memory Model (Memory Order and Barrier) (0) | 2024.01.27 |
| Threads and Memory (0) | 2024.01.25 |
| Pipelining & Branch Optimizations (0) | 2024.01.21 |
| Instruction-Level Parallelism (ILP) (0) | 2024.01.20 |




댓글