References
- Ch3, The Art of Writing Efficient Program
Contents
- CPU Architecture
- Internal concurrency of the CPUs for optimum performance (Super Scalar, ILP)
- Visualizing ILP
CPU Architecture
효율적인 프로그램은 사용 가능한 리소스를 낭비하지 않으며 최대한 활용하는 프로그램이다. 일반적으로 성능(performance)은 특정 목표를 가지고 정의되기 때문에 간단하게 고성능 프로그램을 정의할 수는 없다. 다만, 일반적으로 아래의 두 성능에 대해 크게 관심을 갖는다.
- Computational Performance
- Throughput
이 두 가지 성능은 효율성과 밀접한 관련이 있다.
1초에 얼마나 많은 연산을 수행할 수 있는지에 대한 대답은 사용하는 하드웨어, 리소스의 크기, 프로그램이 이를 얼마나 효율적으로 사용할 수 있는지에 따라서 달라진다.
먼저 단일 스레드에서 CPU를 최대한 활용하는 방법에 대해서 살펴보자. 이를 이해하려면 먼저 CPU가 가지고 있는 리소스에는 어떤 것들이 있는지 알고 있어야 한다.
- Execution Units
- Out-of-Order Scheduling & Retirement
- Instruction Decode & Microcode
- L1 Data Cache
- L2 Cache & Interrupt Servicing
- Memory Ordering & Execution
- Paging
- Branch Prediction
- Instruction Fetch & L1 Cache
위와 같이 다양한 하드웨어 리소스가 존재한다. 실제 인텔 CPU 실리콘을 살펴보면 우리가 CPU의 주요 기능이라고 생각하는 Execution Units, 즉, 덧셈, 곱셈 등 기타 연산들을 수행하는 부분은 전체 실리콘의 1/4도 차지하지 않는다는 것을 볼 수 있다. 그 이외의 것들은 이러한 연산들이 효율적으로 작동하는 것이 목적인 것들이 대부분이다. 많은 하드웨어 구성 요소들이 있지만, 이러한 요소들 중 일부는 대부분 자체적으로 동작하기 때문에 프로그래머가 이를 최대한 활용하기 위해서 별도로 해야 할 일은 없다.
일부 하드웨어에서는 주의 깊게 사용해야 할 필요가 있다. 하지만 이는 대부분 컴파일러의 의해서 수행된다. 하지만 CPU 하드웨어의 절반 이상은 자체적으로 최적화되지 않는다. 따라서 이들이 어떻게 동작하는지, 무엇을 할 수 있는지, 이들이 어떠한 영향을 미치는지 이해해야 프로세서의 성능을 극대화할 수 있다. 자체적으로 잘 동작하는 리소스들도 더 뛰어난 성능을 원한다면 프로그래머가 주의 깊게 사용할 필요가 있다.
Instruction-Level Parallelism (ILP) & Super Scalar
프로세서는 매우 복잡하며, 최상의 효율로 동작하기 위해서는 프로그래머의 주의가 필요하다. 간단한 프로그램을 통해 몇 가지 기본 연산들을 얼마나 빠르게 수행할 수 있는지 google benchmark를 통해서 살펴보자.
사용한 전체 코드는 link에서 확인할 수 있다. 같은 경로의 cmake를 통해 간단히 빌드할 수 있다.
아래 코드는 두 개의 배열의 합을 계산하는 함수에 대한 벤치마크이다.
void BM_add(benchmark::State& state) { srand(1); const unsigned int N = state.range(0); std::vector<unsigned long> v1(N), v2(N); for (size_t i = 0; i < N; ++i) { v1[i] = rand(); v2[i] = rand(); } unsigned long* p1 = v1.data(); unsigned long* p2 = v2.data(); for (auto _ : state) { unsigned long a1 = 0; for (size_t i = 0; i < N; ++i) { a1 += p1[i] + p2[i]; } benchmark::DoNotOptimize(a1); benchmark::ClobberMemory(); } state.SetItemsProcessed(N*state.iterations()); //state.SetBytesProcessed(N*sizeof(unsigned long)*state.iterations()); } #define ARGS \ ->Arg(1<<22) BENCHMARK(BM_add) ARGS; BENCHMARK_MAIN();
이 코드에서 연산의 속도는 피연산자들의 값에 영향을 받지 않는다. 또한, 임의의 값을 사용하므로 입력 값에 민감하더라도 신경쓰지 않아도 된다. 또한, 벡터에 인덱싱하는 속도를 측정하고 싶지는 않으므로 벡터의 raw data를 사용하여 계산에 사용한다 (사실 컴파일러가 v[i]에 대한 표현식을 최적화하여 p[i]와 정확히 동일한 코드를 생성할 가능성이 높다).
벤치마크를 통해 성능을 측정할 때, 원하는 않는 컴파일러 최적화의 가능성에 대해서도 고려해야 한다. 컴파일러는 코드를 살펴본 뒤, 이 코드가 실제로는 아무것도 하지 않는 것과 같다고 판단할 수 있다. 예를 들어, 열심히 계산한 값이 이후에 사용되지 않거나 참조되지 않는다면, 이 계산을 하지 않더라도 결과는 달라지는 것이 없다고 판단할 수 있다는 것이다. a1 변수를 volatile로 선언하면 이러한 원하지 않는 최적화를 방지할 수 있다. 하지만, 이는 루프 자체의 최적화도 막는다. 구글 벤치마크에서 제공하는 DoNotOptimize(a1) 함수를 사용하면 루프 최적화는 막지 않으면서, a1 변수에 대해 원치 않는 최적화는 수행되지 않도록 해준다. 이 함수의 구현 자체는 다음과 같은데, 어셈블리에 익숙하지 않아서 자세히는 이해하지 못했으나 해당 변수의 값이 최적화되어 없어지지 않고 강제로 메모리에 존재할 수 있도록 해주는 것으로 이해하고 있다.
template <class Tp> inline BENCHMARK_ALWAYS_INLINE void DoNotOptimize(Tp& value) { #if defined(__clang__) asm volatile("" : "+r,m"(value) : : "memory"); #else asm volatile("" : "+m,r"(value) : : "memory"); #endif }
이 벤치마크를 실행한 결과는 다음과 같다. 4194304개의 요소에 대한 벡터합 연산이 약 0.113 ms로 측정되었다. 하나의 덧셈 결과를 계산하는데 약 0.27ns가 걸리는 것으로 계산된다.

참고로 DoNotOptimize(a1)을 제거하고 컴파일 한 뒤, 실행하면 벤치마크 결과가 0ns로 측정되는 것을 확인할 수 있다. 즉, 의도치 않은 컴파일러 최적화가 적용되어 정상적인 측정이 이루어지지 않았다는 것을 의미한다.
코드의 성능을 분석하려면 프로세서가 코드를 보는 방식을 이해해야 하는데, 코드에서는 단순 덧셈보다 더 많은 것들이 발생한다. 두 입력 배열의 값은 메모리에 저장되어 있지만, 덧셈이나 곱셈 연산은 레지스터에 저장된 값 사이에서 수행된다. 일부 연산의 경우에는 레지스터와 메모리 사이에서 수행되기도 한다. 그럼 이제 루프의 반복이 어떻게 수행되는지 단계별로 살펴보자. 루프의 반복이 시작될 때 인덱스 변수 i는 CPU 레지스터에 있고, 배열 요소 v1[i] 및 v2[i]는 메모리에 위치하게 된다.

연산을 수행하기 전에 입력 값은 레지스터로 옮겨져야 하므로, 각 입력에 대한 레지스터와 덧셈 결과를 저장할 레지스터를 할당한다. 따라서, 루프의 반복에서 수행되는 첫 번째 명령어는 입력 값 중 하나를 레지스터로 로드하는 것이다.

다음 명령어는 두 번째 입력을 로드하는 것이다.

그러고 나면 덧셈이나 곱셈 연산을 수행할 준비가 되었고, 해당 명령어를 수행하여 레지스터로 저장하게 된다.

아래의 한 줄의 코드가 하드웨어 명령어로 변환된 이후에 위의 과정(+ 다음 루프를 준비하는 명령 포함)들을 생성하게 된다.
a1 += p1[i] + p2[i];
효율성 측면에서 마지막 단계인 덧셈에 초점을 맞추어 살펴보자. CPU는 나노초 이내에 두 개의 숫자를 더하거나 곱할 수 있다. 앞서 벤치마크 결과를 봤듯이 하나의 덧셈 결과를 계산하는데 0.27나노초가 소요되었다. CPU에서는 많은 트랜지스터들이 명령을 처리하고 실행하는데 할당되어 있기 때문에 이보다 더 많은 것들을 동시에 할 수 있다. 아래의 두 벤치마크(곱셈, 덧셈+곱셈) 성능을 추가로 살펴보자.
void BM_multiply(benchmark::State& state) { srand(1); const unsigned int N = state.range(0); std::vector<unsigned long> v1(N), v2(N); for (size_t i = 0; i < N; ++i) { v1[i] = rand(); v2[i] = rand(); } unsigned long* p1 = v1.data(); unsigned long* p2 = v2.data(); for (auto _ : state) { unsigned long a1 = 0; for (size_t i = 0; i < N; ++i) { a1 += p1[i] * p2[i]; } benchmark::DoNotOptimize(a1); benchmark::ClobberMemory(); } state.SetItemsProcessed(N*state.iterations()); //state.SetBytesProcessed(N*sizeof(unsigned long)*state.iterations()); } void BM_add_multiply(benchmark::State& state) { srand(1); const unsigned int N = state.range(0); std::vector<unsigned long> v1(N), v2(N); for (size_t i = 0; i < N; ++i) { v1[i] = rand(); v2[i] = rand(); } unsigned long* p1 = v1.data(); unsigned long* p2 = v2.data(); for (auto _ : state) { unsigned long a1 = 0, a2 = 0; for (size_t i = 0; i < N; ++i) { a1 += p1[i] + p2[i]; a2 += p1[i] * p2[i]; } benchmark::DoNotOptimize(a1); benchmark::DoNotOptimize(a2); benchmark::ClobberMemory(); } state.SetItemsProcessed(N*state.iterations()); //state.SetBytesProcessed(N*sizeof(unsigned long)*state.iterations()); }

덧셈과 곱셈만 수행하는 벤치마크의 성능이 각각 3.73G/s, 3.1G/s로 측정되는데, 덧셈과 곱셈을 모두 수행하는 벤치마크의 성능이 2.9G/s로 측정된다. 즉, 수행하는 연산의 수가 두 배가 되었지만, 그 성능은 두 배 감소하지 않는다는 것을 보여준다.
조금 더 많은 연산들을 수행하는 벤치마크를 통해 다시 한 번 성능을 측정해보자.
void BM_add_multiply_sub_shift(benchmark::State& state) { srand(1); const unsigned int N = state.range(0); std::vector<unsigned long> v1(N), v2(N); for (size_t i = 0; i < N; ++i) { v1[i] = rand(); v2[i] = rand(); } unsigned long* p1 = v1.data(); unsigned long* p2 = v2.data(); for (auto _ : state) { unsigned long a1 = 0, a2 = 0; unsigned long a3 = 0, a4 = 0; for (size_t i = 0; i < N; ++i) { a1 += p1[i] + p2[i]; a2 += p1[i] * p2[i]; a3 += p1[i] << 2; a4 += p2[i] - p1[i]; } benchmark::DoNotOptimize(a1); benchmark::DoNotOptimize(a2); benchmark::DoNotOptimize(a3); benchmark::DoNotOptimize(a4); benchmark::ClobberMemory(); } state.SetItemsProcessed(N*state.iterations()); //state.SetBytesProcessed(N*sizeof(unsigned long)*state.iterations()); }

4개의 연산을 수행하는 함수의 성능은 1개의 연산을 수행하는 함수의 성능보다 4배 더 느려지지는 않는 것을 확인할 수 있다. 따라서, 프로세서는 한 번에 하나의 명령을 실행한다고 보는 관점은 잘못된 것이라고 판단할 수 있다.
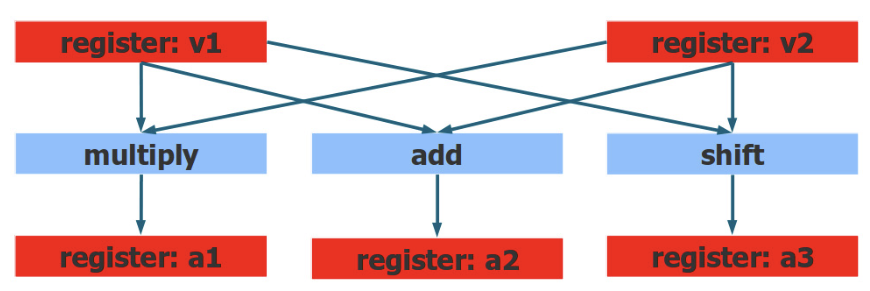
피연산자가 이미 레지스터에 로드되었다면, 프로세서는 여러 연산을 한 번에 실행할 수 있다. 이것이 바로 명령어 수준에서의 병렬화, Instruction-Level Parallelism(ILP)이다. 물론, 한 번에 실행할 수 있는 연산의 수에는 한계가 존재한다. 프로세서에는 정수 연산을 수행할 수 있는 execution units이 많다. 따라서, 한 번의 반복에서 더 많은 명령을 처리할 수 있도록 하는 것이 좋다.
이렇게 CPU 내 여러 연산 장치들을 동시에 활용하여 명령어를 동시에 실행하는 기술을 슈퍼스칼라(superscalar)라고 부른다.
프로세서가 한 번에 실행할 수 있는 명령어의 수는 CPU와 어떤 명령을 수행하는지에 따라 다르다. 하지만, 아래와 같이 많은 명령어들을 수행하는 벤치마크의 경우에는 단일 덧셈을 수행하는 벤치마크의 성능보다 눈에 띄게 느려진 것을 확인할 수 있다.
void BM_instructions(benchmark::State& state) { srand(1); const unsigned int N = state.range(0); std::vector<unsigned long> v1(N), v2(N); for (size_t i = 0; i < N; ++i) { v1[i] = rand(); v2[i] = rand(); } unsigned long* p1 = v1.data(); unsigned long* p2 = v2.data(); for (auto _ : state) { unsigned long a1 = 0, a2 = 0; unsigned long a3 = 0, a4 = 0; unsigned long a5 = 0, a6 = 0; for (size_t i = 0; i < N; ++i) { a1 += p1[i] + p2[i]; a2 += p1[i] * p2[i]; a3 += p1[i] << 2; a4 += p2[i] - p1[i]; a5 += (p2[i] << 1)*p2[i]; a6 += (p2[i] - 3)*p1[i]; } benchmark::DoNotOptimize(a1); benchmark::DoNotOptimize(a2); benchmark::DoNotOptimize(a3); benchmark::DoNotOptimize(a4); benchmark::DoNotOptimize(a5); benchmark::DoNotOptimize(a6); benchmark::ClobberMemory(); } state.SetItemsProcessed(N*state.iterations()); //state.SetBytesProcessed(N*sizeof(unsigned long)*state.iterations()); }

지금까지 살펴본 결과를 통해 하드웨어 활용 측면에서 BM_add 벤치마크에서와 같이 덧셈만 수행하는 코드가 얼마나 비효율적인지 알 수 있다. CPU는 한 번에 반복에서 여러 개의 서로 다른 연산을 수행할 수 있으며, 최신 프로세서의 경우에는 그 능력이 더욱 뛰어날 것이다. 지금까지 실험한 정수 연산 이외에도 double 또는 float에 대한 명령을 실행하는 별도의 부동소수점 하드웨어와 MMX, SSE, AVX 등 다른 특별한 명령어를 수행하는 벡터 처리 장치도 있으니, 이를 활용하는 것도 중요하다.
Visualizing Instruction-Level Parallelism
지금까지 병렬로 명령어를 실행할 수 있는 CPU 능력을 벤치마크 성능을 통해 간접적으로 확인했다. LLVM의 툴체인 중 하나인 Machine Code Analyzer (MCA)를 사용하면 이를 직접적으로 확인할 수 있다. 이 툴은 어셈블리 코드를 통해 명령어가 실행되는 방법, 어떤 명령어가 지연이되고 병목인지 등에 대한 정보를 리포트한다. 툴에 대한 자세한 내용은 link에서 확인해볼 수 있다.
이 툴을 사용하려면 먼저 코드에서 이 툴이 살펴볼 부분을 지정해주어야 한다.
#define MCA_START asm volatile("# LLVM-MCA-BEGIN"); #define MCA_END asm volatile("# LLVM-MCA-END"); void BM_add(benchmark::State& state) { srand(1); const unsigned int N = state.range(0); std::vector<unsigned long> v1(N), v2(N); for (size_t i = 0; i < N; ++i) { v1[i] = rand(); v2[i] = rand(); } unsigned long* p1 = v1.data(); unsigned long* p2 = v2.data(); for (auto _ : state) { unsigned long a1 = 0; for (size_t i = 0; i < N; ++i) { MCA_START a1 += p1[i] + p2[i]; MCA_END } benchmark::DoNotOptimize(a1); benchmark::ClobberMemory(); } state.SetItemsProcessed(N*state.iterations()); //state.SetBytesProcessed(N*sizeof(unsigned long)*state.iterations()); }
llvm-mca은 어셈블리 코드를 입력으로 받는다. 따라서, 아래와 같은 명령어를 통해 llvm-mca를 실행하여 결과를 얻을 수 있다.
| $ clang++ ../01_superscalar.cpp -I_deps/benchmark-src/include -g -O3 -S -o - | llvm-mca --timeline |
리눅스와 macos의 결과가 조금 다른데, ubuntu 20.04에서 얻은 타임라인 결과는 다음과 같다.

가로축은 사이클 단위의 시간이며, llvm-mca는 마킹된 코드(START와 END 사이의 코드 조각)를 10회 반복 실행하는 것으로 시뮬레이션한다. 각 명령어는 코드의 일련 번호와 몇 번째 반복인지를 나타내는 인덱스로 식별되는데, 첫 번째 반복의 첫 번째 명령어는 [0,0]이며 마지막 명령어는 [9,2]이다. 즉, 코드 조각으로부터 생성된 기계어가 반복 당 3개의 명령어라는 것을 알 수 있다. 위 타임라인 결과에 따르면 전체 시퀀스는 30 사이클이 걸린다.
참고로 타임라인에서 각 문자의 의미는 다음과 같다.
- D: instruction dispatched
- e: instruction executing
- E: instruction executed
- R: instruction retired
- =: instruction already dispatched, waiting to be executed
- -: instruction executed, waiting to be retired
다음은 아래 코드에 대한 타임라인 결과를 살펴보자.
for (size_t i = 0; i < N; ++i) { MCA_START a1 += p1[i] + p2[i]; a2 += p1[i] * p2[i]; MCA_END }
결과가 길어서 일부만 가져왔다.
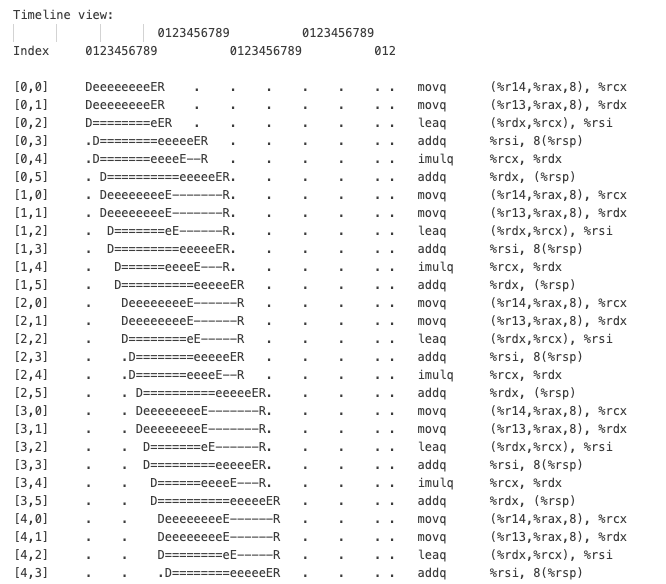
한 번의 반복에서 더 많은 명령어가 실행되는 것을 볼 수 있다. 각 반복에서는 6개의 명령어가 실행된다. 그리고 10번의 반복이 총 43 사이클에 끝이난다. 프로세서는 두 배나 많은 명령어를 처리했지만, 이에 걸리는 시간이 두 배로 증가하지 않았다.
'프로그래밍 > Optimizations' 카테고리의 다른 글
| Lock-Based, Lock-Free, Wait-Free Program (0) | 2024.02.02 |
|---|---|
| Memory Model (Memory Order and Barrier) (0) | 2024.01.27 |
| Threads and Memory (0) | 2024.01.25 |
| Cache (0) | 2024.01.22 |
| Pipelining & Branch Optimizations (0) | 2024.01.21 |




댓글