References
파이토치의 autograd는 파이토치가 머신러닝 프로젝트를 빌드하는데 유연하고 빠르게 만들어주는 것들 중 하나입니다. 이는 복잡한 계산인 mutiple partial derivaties (referred to as gradients)를 빠르고 쉽게 계산할 수 있도록 해줍니다. 이 연산은 backpropagation 기반의 뉴럴 네트워크 학습의 핵심입니다.
autograd는 런타임에서 동적으로 연산을 추적합니다. 즉, 모델에 decision branches나 길이를 런타임 전까지 알 수 없는 loop가 있는 경우에도 연산은 여전히 올바르게 추적되고 올바른 gradients를 얻을 수 있습니다. 이 때문에 파이토치는 엄격히 구조화된 모델의 정적 분석에 의존하는 다른 프레임워크보다 더 많은 유연성을 제공할 수 있습니다.
What Do We Need Autograd For ?
그렇다면 autograd가 왜 필요한 것일까요?
머신러닝 모델은 입력과 출력이 있는 함수입니다.
A Simple Example
간단한 예제를 통해서 autograd를 어떻게 사용하고 실제로 무엇을 하는지 살펴보겠습니다.
%matplotlib inline
import torch
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import math우선 필요한 패키지들을 import 합니다.
그리고, \([0, 2\pi]\) 구간에서 균일한 간격의 값들로 구성된 input 텐서를 생성하고, required_grad=True로 지정해줍니다. required_grad 플래그를 설정하면, 이후의 모든 연산에서 autograd가 해당 연산의 output 텐서에 연산의 기록을 축적합니다.
a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
print(a)
다음으로, 한 가지 연산(sin)을 수행하고 입력에 대한 출력을 그래프로 그려보겠습니다.
b = torch.sin(a)
plt.plot(a.detach(), b.detach())
이제 출력 텐서인 b를 조금 자세히 살펴보겠습니다. 텐서 b를 출력해보면 computation history를 추적하는 indicator를 확인할 수 있습니다.
print(b)
grad_fn은 우리가 backpropagation step과 gradients를 계산할 때, 이 텐서의 모든 입력에 대해 sin(x)의 도함수를 계산해야한다는 힌트를 제공합니다.
연산을 몇 번 더 진행해보겠습니다.
c = 2 * b
print(c)
d = c + 1
print(d)
마지막으로, single-element output을 계산합니다.
out = d.sum()
print(out)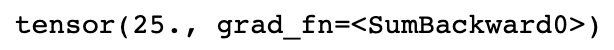
위의 텐서들에 저장된 각 grad_fn을 사용하면 grad_fn의 next_functions 프로퍼티를 사용하여 input까지의 모든 연산을 되돌아가며 수행할 수 있습니다.
print('d:')
print(d.grad_fn)
print(d.grad_fn.next_functions)
print(d.grad_fn.next_functions[0][0].next_functions)
print(d.grad_fn.next_functions[0][0].next_functions[0][0].next_functions)
print(d.grad_fn.next_functions[0][0].next_functions[0][0].next_functions[0][0].next_functions)
print('\nc:')
print(c.grad_fn)
print('\nb:')
print(b.grad_fn)
print('\na:')
print(a.grad_fn)
위의 코드에서 d에 있는 grad_fn와 next_functions 프로퍼티를 사용하여 이전의 모든 텐서에 대한 gradient function을 보여주고 있습니다. 여기서 a.grad_fn은 None인데, 이는 a는 input이기 때문에 연산 기록이 없기 때문입니다.
이제 output에 대해서 backward() 메소드를 호출하면, gradients를 계산할 수 있고, input의 grad 프로퍼티를 통해 gradients의 계산값이 어떻게 되는지 살펴볼 수 있습니다.
out.backward()
print(a.grad)
plt.plot(a.detach(), a.grad.detach())

a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
b = torch.sin(a)
c = 2 * b
d = c + 1
out = d.sum()위의 코드는 연산의 과정을 다시 한 번 나타낸 것입니다.
사실, 상수항은 도함수를 구할 때 아무런 영향을 미치지 않기 때문에 \(c = 2 * b = 2 * \sin(a)\) 에 대한 도함수 \(2 * cos(a)\)를 계산하게 됩니다. 이는 위에서 그려진 input에 대한 output의 그래프에 해당합니다.
Differentiation in Autograd
또 다른 예제를 파이토치에서 제공하고 있어서, 다시 한 번 autograd가 어떻게 gradients를 구하는지 살펴보겠습니다.
먼저 requires_grad=True로 지정된 두 개의 텐서 a와 b를 생성합니다. requires_grad는 autograd가 모든 연산을 추적하도록 합니다.
a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)그리고 아래의 연산을 수행하는 텐서 Q를 생성합니다.
\[Q = 3a^3 - b^2\]
Q = 3*a**3 - b**2
텐서 a와 b가 뉴럴 네트워크의 파라미터, Q가 output에 대한 error라고 가정해봅시다. 학습 시, 우리는 파라미터에 대한 error의 gradients를 구해야 합니다. 즉, 아래의 gradient를 구해야 합니다.
\[\begin{align*} \frac{\partial Q}{\partial a} = 9a^2 \\ \frac{\partial Q}{\partial b} = -2b \end{align*}\]
텐서 Q에 대해 backward() 메소드를 호출하면 autograd는 위의 gradients를 계산하고 각각에 대응되는 텐서의 .grad 프로퍼티에 저장합니다.
이때, Q.backward()의 gradient 인자를 명시적으로 전달해야 하는데, Q가 벡터이기 때문입니다. gradient는 Q와 동일한 shape의 텐서이고, 이는 아래와 같이 Q 자신에 대한 gradient를 나타냅니다.
\[\frac{dQ}{dQ} = 1\]
이는 Q에 대해 스칼라고 총합을 구하고, backward를 호출하는 Q.sum().backward()와 동일합니다.
external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)Gradients 결과는 a.grad와 b.grad에 이제 저장됩니다.
# check if collected gradients are correct
print(9*a**2 == a.grad)
print(-2*b == b.grad)
Vector Calculus using autograd
수학적으로 vector valued function \(\vec{y} = f(\vec{x})\) 가 있을 때, \(\vec{x}\)에 대한 \(\vec{y}\)의 gradient는 Jacobian matrix \(J\) 입니다.
\[J = \begin{pmatrix} \frac{\partial \mathbb{y}}{\partial x_1} & \cdots & \frac{\partial \mathbb{y}}{\partial x_n} \end{pmatrix} = \begin{pmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{pmatrix} \]
일반적으로 torch.autograd는 vector-Jacobian product를 연산하기 위한 엔진입니다. 즉, 주어진 임의의 벡터 \(\vec{v}\)에 대해 \(J^T\cdot\vec{v}\)를 계산합니다.
만약 \(\vec{v}\)가 스칼라 함수 \(l = g(\vec{y})\)의 gradient라면,
\[\vec{v} = \begin{pmatrix} \frac{\partial l}{\partial y_1} & \cdots & \frac{\partial l}{\partial y_m} \end{pmatrix}^T\]
이고, chain rule에 의해서 vector-Jacobian product는 \(\vec{x}\)에 대해 \(l\)의 gradient가 됩니다.
\[J^T\cdot\vec{v} = \begin{pmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{pmatrix} \begin{pmatrix} \frac{\partial l}{\partial y_1} \\ \vdots \\ \frac{\partial l}{\partial y_m} \end{pmatrix} = \begin{pmatrix} \frac{\partial l}{\partial x_1} \\ \vdots \\ \frac{\partial l}{\partial x_n} \end{pmatrix} \]
이러한 vector-Jacobian product의 특징이 바로 위의 예제 코드에서 external_grad를 사용한 것이며, external_grad는 \(\vec{v}\)에 해당합니다.
Computational Graph
개념적으로 autograd는 data(tensors)의 record를 기록하고 Function 객체으로 구성된 DAG(directed acyclic graph)에서 실행된 모든 연산을 기록합니다. DAG에서 리프 노드(leaves)는 input tensors이며, 루트(roots)는 output tensors 입니다. 루트에서 리프노드까지의 그래프를 추적하여, chain rule을 사용하여 gradients를 자동으로 계산할 수 있습니다.
[pytorch] Tutorial - Automatic Differentiation (autograd)
[pytorch] Tutorial - Automatic Differentiation (autograd)
References Official Pytorch Tutorial (link) torch.autograd Neural network를 학습할 때, 가장 많이 사용되는 알고리즘은 backpropagation 입니다. 이 알고리즘에서 파라미터, 즉, 모델의 weights는 주어진 파라미터에 대
junstar92.tistory.com
이전 포스팅에서 autograd의 computational graph에 대해 언급하며 forward pass와 backword pass에서 autograd가 수행하는 것들에 대해 정리해두었으니 필요하시면 참조바랍니다 !
아래 그림은 DAG를 시각적으로 표현하고 있습니다.
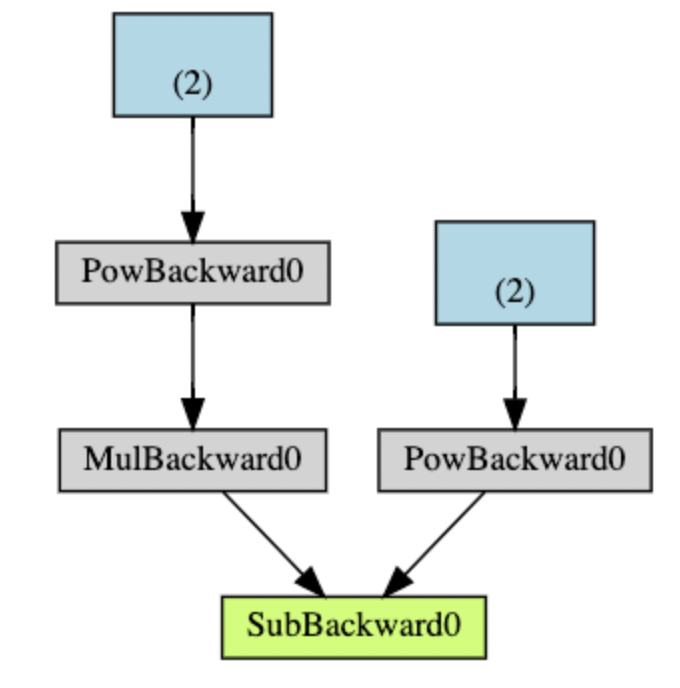
이 그래프에서 화살표는 forward pass의 방향입니다. 노드는 forward pass에서 각 연산의 backward functions을 나타내며, 파란색의 리프 노드는 위의 예제에서 텐서 a와 b에 해당합니다.
torch github의 README.md를 보시면, 다음과 같이 graph 형성 과정을 보여주고 있습니다.

특히, 다른 프레임워크와는 다르게 동적으로 backward graph를 구성한다고 언급하고 있습니다.
Exclusion from the DAG
torch.autograd는 requires_grad 플래그가 True로 설정된 모든 텐서에 대한 연산을 추적합니다. 만약 gradient가 필요없는 텐서라면 이 속성을 False로 설정하여 gradient computation DAG에서 제외시키면 됩니다.
만약 두 텐서 중 하나의 텐서만 requires_grad=True로 설정되었다면, 이 텐서들에 대한 output 텐서는 gradients를 필요로 하게 됩니다.
x = torch.rand(5, 5)
y = torch.rand(5, 5)
z = torch.rand((5, 5), requires_grad=True)
a = x + y
print(f"Does `a` require gradients? : {a.requires_grad}")
b = x + z
print(f"Does `b` require gradients? : {b.requires_grad}")
뉴럴 네트워크에서 gradients를 계산할 필요가 없는 파라미터를 보통 frozen parameters라고 부릅니다. 만약 어떤 파라미터의 gradient 계산이 필요하지 않다는 것을 미리 알고 있는 경우, 모델의 일부를 freeze하여 성능상의 이점을 얻을 수 있습니다 (연산량 감소).
DAG로부터 연산 추적을 제외하는 것이 중요한 일반적인 예시로는 pretrained network를 finetuning하는 것이 있습니다. Finetuning에서는 일반적으로 classifier layers만 수정하여 새로운 라벨에 대해서만 예측을 수행합니다.
Turning Autograd Off and On
바로 위에서 언급한 것처럼 autograd 활성화 여부를 미세하게 제어해야 하는 상황이 있습니다. 상황에 따라 여러 방법들이 있지만, 가장 간단한 방법은 텐서의 requires_grad 플래그를 직접 변경하는 것입니다.
a = torch.ones(2, 3, requires_grad=True)
print(a)
b1 = 2 * a
print(b1)
a.requires_grad = False
b2 = 2 * a
print(b2)
위의 코드 실행 결과에서 b1 텐서가 grad_fn (i.e, a traced computation history)를 가지고 있다는 것을 볼 수 있습니다. 이는 예상하듯이 텐서 a로부터 유도되며 텐서 a의 autograd는 활성화되어 있습니다. 여기서 명시적으로 a.requires_grad = False를 통해 autograd를 비활성화해주면 연산 기록은 더 이상 추적되지 않으며, b2의 결과와 같이 나타납니다.
만약 일시적으로 autograd를 비활성화해야할 때는 torch.no_grad(): 를 사용하는 것이 좋습니다.
a = torch.ones(2, 3, requires_grad=True) * 2
b = torch.ones(2, 3, requires_grad=True) * 3
c1 = a + b
print(c1)
with torch.no_grad():
c2 = a + b
print(c2)
c3 = a * b
print(c3)
torch.no_grad()는 함수나 메소드의 데코레이터(decorator)로도 사용될 수 있습니다.
def add_tensors1(x, y):
return x + y
@torch.no_grad()
def add_tensors2(x, y):
return x + y
a = torch.ones(2, 3, requires_grad=True) * 2
b = torch.ones(2, 3, requires_grad=True) * 3
c1 = add_tensors1(a, b)
print(c1)
c2 = add_tensors2(a, b)
print(c2)
반대로, autograd가 비활성화되어 있을 때 autograd를 활성화시켜주는 torch.enable_grad()라는 context manager도 있습니다. 이 또한 데코레이터로 사용될 수 있습니다.
마지막으로, gradient tracing이 활성화된 텐서가 있을 때, autograd가 비활성화된 복사본이 필요할 수 있습니다. 이때, 텐서 객체의 detach() 메소드를 사용하면 computation history로부터 분리된 텐서의 복사본을 생성할 수 있습니다.
x = torch.rand(5, requires_grad=True)
y = x.detach()
print(x)
print(y)
위에서 살펴본 예제 코드 중, matplotlib으로 텐서를 그래프로 표시할 때 이 메소드를 사용하여 인자로 전달한 것을 확인할 수 있습니다.
(matplotlib은 numpy 배열을 입력으로 요구하지만, requires_grad=True인 텐서는 텐서에서 numpy 배열로 암시적 변환이 허용되지 않기 때문)
Autograd and In-place Operations
지금까지 모든 예제에서 연산을 수행할 때 중간 값을 다른 변수에 저장하여 캡처하였습니다. 이처럼 autograd는 gradients를 계산하기 위해서 이와 같은 중간 값이 필요합니다. 이러한 이유로 autograd를 사용할 때는 in-place operations 사용에 주의해야 합니다. 만약 in-place 연산을 사용하면 backward()를 호출하여 도함수를 계산하는데 필요한 정보가 손상될 수 있습니다. 파이토치에서는 autograd가 활성화된 리프 변수에 대해 in-place 연산을 수행할 때, 아래와 같이 작업을 중단시킵니다.
a = torch.linspace(0., 2. * math.pi, steps=25, requires_grad=True)
torch.sin_(a)
Autograd Profiler
Autograd는 연산의 각 단계의 세부사항을 추적합니다. 이러한 연산 기록과 timing information을 결합하여 편리한 프로파일러를 만들 수 있으며, autograd에는 이러한 기능이 내장되어 있습니다.
device = torch.device('cpu')
run_on_gpu = False
if torch.cuda.is_available():
device = torch.device('cuda')
run_on_gpu = True
x = torch.randn(2, 3, requires_grad=True)
y = torch.rand(2, 3, requires_grad=True)
z = torch.ones(2, 3, requires_grad=True)
with torch.autograd.profiler.profile(use_cuda=run_on_gpu) as prf:
for _ in range(1000):
z = (z / x) * y
print(prf.key_averages().table(sort_by='self_cpu_time_total'))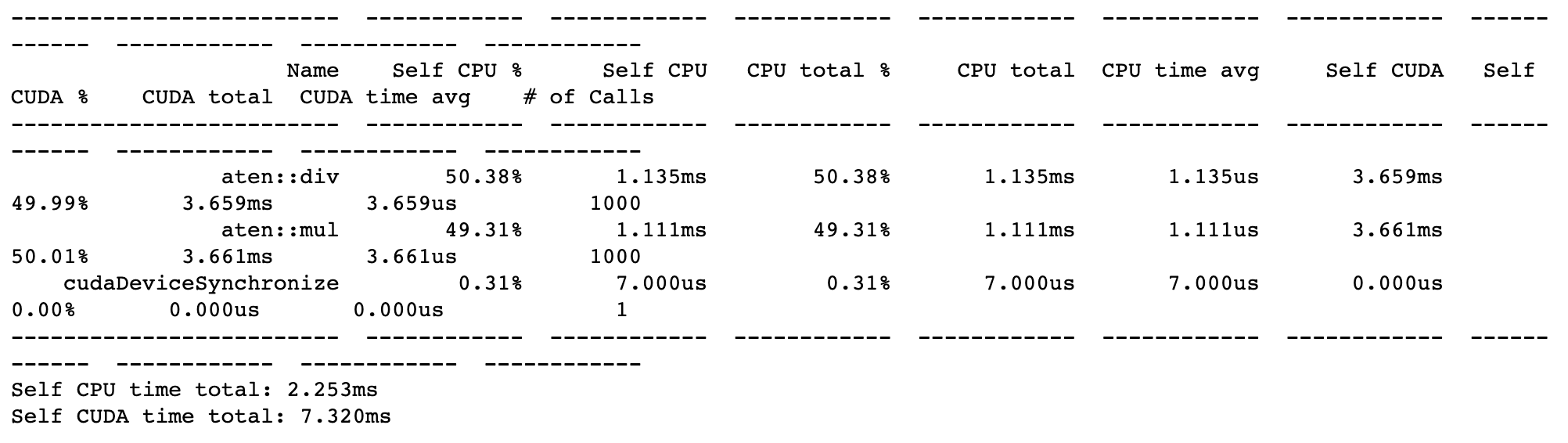
이 API에 대한 자세한 내용은 문서(link)를 참조바랍니다.
'ML & DL > pytorch' 카테고리의 다른 글
| [pytorch] 커스텀 연산 with autograd (0) | 2022.12.26 |
|---|---|
| [pytorch] Tensors (0) | 2022.12.01 |
| [pytorch] Tutorial - Optimizing Model Parameters (0) | 2022.11.30 |
| [pytorch] Tutorial - Automatic Differentiation (autograd) (0) | 2022.11.29 |
| [pytorch] Tutorial - Build the Neural Network (0) | 2022.11.29 |




댓글