References
- Fluent Python
Contents
- Operator Overloading
- @ Infix Operator
- Augmented Assignment Operator Overloading
연산자 오버로딩은 사용자 정의 객체가 +와 | 같은 중위 연산자, -와 ~와 같은 단항 연산자를 사용할 수 있게 해줍니다. 파이썬에서는 여기에서 더 나아가 함수 호출(()), 속성 접근(.), 항목 접근 및 슬라이싱([])도 연산자로 구현되어 있지만, 이번 포스팅에서는 단항 연산자와 중위 연산자에 대해서 살펴보겠습니다.
import math
class Vector:
def __init__(self, x=0, y=0):
self.x = x
self.y = y
def __repr__(self):
return f'Vector({self.x!r}, {self.y!r})'
def __abs__(self):
return math.hypot(self.x, self.y)
def __bool__(self):
return bool(abs(self))
def __add__(self, other):
x = self.x + other.x
y = self.y + other.y
return Vector(x, y)
def __mul__(self, scalar):
return Vector(self.x * scalar, self.y * scalar)예전 포스팅에서 구현한 기본 Vector 클래스는 간단한 연산자를 구현하고 있습니다. __add__()와 __mul__() 메소드는 스페셜 메소드가 연산자 오버로딩을 지원하는 방법을 보여주기 위해 작성되었지만, 여기에는 간과된 미묘한 문제가 있습니다.
from array import array
import math
class Vector2d:
__match_args__ = ('x', 'y')
typecode = 'd'
def __init__(self, x, y):
self.__x = float(x)
self.__y = float(y)
@property
def x(self):
return self.__x
@property
def y(self):
return self.__y
def __len__(self):
return 2
def __iter__(self):
return (i for i in (self.x, self.y))
def __repr__(self):
class_name = type(self).__name__
return '{}({!r}, {!r})'.format(class_name, *self)
def __str__(self):
return str(tuple(self))
def __bytes__(self):
return (bytes([ord(self.typecode)]) +
bytes(array(self.typecode, self)))
def __eq__(self, other):
return tuple(self) == tuple(other)
def __hash__(self):
return hash(self.x) ^ hash(self.y)
def __abs__(self):
return math.hypot(self.x, self.y)
def __bool__(self):
return bool(abs(self))
def angle(self):
return math.atan2(self.y, self.x)
def __format__(self, fmt_spec=''):
if fmt_spec.endswith('p'):
fmt_spec = fmt_spec[:-1]
coords = (abs(self), self.angle())
outer_fmt = '<{}, {}>'
else:
coords = self
outer_fmt = '({}, {})'
components = (format(c, fmt_spec) for c in coords)
return outer_fmt.format(*components)
@classmethod
def frombytes(cls, octets):
typecode = chr(octets[0])
memv = memoryview(octets[1:]).cast(typecode)
return cls(*memv)그리고, 위의 Vector2d 클래스에 Vector2d.__eq__() 메소드가 Vector2d(3, 4) == [3, 4]를 True라고 판단합니다. 이러한 문제들도 이번 포스팅에서 다루어보도록 하겠습니다.
Operator Overloading
연산자 오버로딩은 남용되거나, 프로그래머를 혼란스럽게 만들거나, 버그를 만들거나, 예상치 못한 성능상의 병목이 될 수도 있습니다. 그렇지만 잘 사용하면 코드의 가독성이 향상되고 만족스러운 API를 구현할 수 있습니다. 파이썬은 다음과 같은 제약 사항을 두어 유연성, 사용성, 안정성을 적절히 유지합니다.
- 내장 자료형에 대한 연산자는 오버로딩할 수 없다
- 새로운 연산자를 생성할 수 없으며, 기존 연산자를 오버로딩만 할 수 있다
- is, and, or, not 연산자는 오버로딩할 수 없다 (&, |, ~ 비트 연산자는 가능하다)
Unary Operators
파이썬 레퍼런스 문서의 'Unary arithmetic and bitwise operations'(link)에 나오는 3개의 단항 연산자와 및 이 연산자와 연관된 스페셜 메소드는 다음과 같습니다.
- - (__neg__) :
단항 산술 부정. x가 -2면, -x는 2이다. - + (__pos__) :
단항 산술 덧셈. 일반적으로 x와 +x는 동일하지만, 그렇지 않은 경우도 있다. - ~ (__invert__) :
정수형의 비트 반전. ~x는 -(x+1)로 정의된다. x가 2라면, ~x는 -3이다.
파이썬 레퍼런스 문서의 'Data Model' 챕터(link)에서는 내장 함수인 abs()도 단항 연산자로 나열합니다. abs() 내장 함수는 __abs__() 스페셜 메소드와 연관되어 있습니다.
단항 연산자는 구현하기 쉽습니다. 단지 self 인수 하나를 받는 적절한 스페셜 메소드를 구현하면 됩니다. 클래스에 논리적으로 합당한 연산을 수행해야 하는데, 특히 '언제나 새로운 객체를 반환해야 한다'는 연산자의 핵심 규칙을 지켜야 합니다. 즉, self를 수정하지 말고 적절한 자료형의 객체를 새로 생성해서 반환해야 합니다.
-와 +의 경우, 결과는 아마도 self와 같은 클래스의 객체일 것입니다. +의 경우 일반적으로 self의 사본을 반환하는 것이 좋습니다. abs()의 경우 스칼라형 숫자가 결과로 나옵니다. ~의 경우 정수 이외의 피연산자에 적용하면 어떤 값이 나와야 하는지 확답하기는 어렵습니다. 예를 들어, 객체 관계 매핑(ORM)에서 ~를 사용한다면 SQL의 WHERE 절을 부정한 결과를 반환하는 것이 타당할 것입니다.
[Python] Special Methods for Sequences
from array import array
import reprlib
import math
import operator
import functools
import itertools
class Vector:
typecode = 'd'
def __init__(self, components):
# 'protected' 객체 속성 self._components는 벡터 요소를 배열로 저장
self._components = array(self.typecode, components)
def __iter__(self):
# 반복할 수 있도록 self._components의 반복자를 반환
return iter(self._components)
def __repr__(self):
# self._components를 제한된 길이로 표현하기 위해 reprlib.repr()를 사용
# array('d', [0.0, 1.0, ...]) 형태로 출력
components = reprlib.repr(self._components)
# 문자열을 Vector 생성자에 전달할 수 있도록 문자열 "array('d',"와
# 마지막 괄호를 제거
components = components[components.find('['):-1]
return f'Vector({components})'
def __str__(self):
return str(tuple(self))
def __bytes__(self):
return (bytes([ord(self.typecode)]) +
bytes(self._components)) # self._components에서 바로 bytes 객체 생성
def __eq__(self, other):
return (len(self) == len(other) and
all(a == b for a, b in zip(self, other)))
def __hash__(self):
# 각 요소의 해시를 계산하기 위한 제너레이터 표현식을 생성
hashes = (hash(x) for x in self._components)
# xor 함수와 hashes를 전달하여 reduce() 함수 호출, 세 번째 인수 0은 초기값
return functools.reduce(operator.xor, hashes, 0)
def __abs__(self):
# 파이썬 3.8부터 math.hypot은 n차원 포인트를 받을 수 있음, 파이썬 3.8 이전이라면
# math.sqrt(sum(x * x for x in self)) 로 작성
return math.hypot(*self)
def __bool__(self):
return bool(abs(self))
def __len__(self):
return len(self._components)
def __getitem__(self, key):
if isinstance(key, slice): # if index's type is slice
# 객체의 클래스(Vector)를 가져옴
cls = type(self)
# _components 배열의 슬라이스로부터 Vector 객체 생성
return cls(self._components[key])
# if index's type is Integral
index = operator.index(key)
# _components에서 해당 항목을 가져와서 반환
return self._components[index]
# __getattr__에 의해 지원되는 dynamic attributes의 매칭 패턴
__match_args__ = ('x', 'y', 'z', 't')
def __getattr__(self, name):
# Vector 클래스를 가져옴
cls = type(self)
try:
# __match_args__에서 name의 위치를 가져옴
pos = cls.__match_args__.index(name)
# name을 찾지 못했을 때 .index(name)는 ValueError를 발생시킴
except ValueError:
# name을 찾지 못하면 pos를 -1로 설정
pos = -1
# pos가 유효한 인덱스라면 해당 항목 반환
if 0 <= pos < len(self._components):
return self._components[pos]
# 여기까지 도달하면 문제가 발생했다는 것이고, AttributeError를 발생시킴
msg = f'{cls.__name__!r} object has no attirbute {name!r}'
raise AttributeError(msg)
def __setattr__(self, name, value):
cls = type(self)
if len(name) == 1:
if name in cls.__match_args__:
error = 'readonly attribute {attr_name!r}'
elif name.islower():
error = "can't set attributes 'a' to 'z' in {cls_name!r}"
else:
error = ''
if error:
msg = error.format(cls_name=cls.__name__, attr_name=name)
raise AttributeError(msg)
super().__setattr__(name, value)
# 특정 좌표에 대한 각좌표를 계산
def angle(self, n):
r = math.hypot(*self[n:])
a = math.atan2(r, self[n-1])
if (n == len(self) - 1) and (self[-1] < 0):
return math.pi * 2 - a
else:
return a
# 모든 각좌표를 계산하는 제너레이터 표현식을 생성
def angles(self):
return (self.angle(n) for n in range(1, len(self)))
def __format__(self, fmt_spec=''):
if fmt_spec.endwidth('h'):
fmt_spec = fmt_spec[:-1]
# itertools.chain() 함수를 이용해서 크기와 각좌표를 차례로 반복하는
# 제너레이터 표현식 생성
coords = itertools.chain([abs(self)],
self.angles())
outer_fmt = '<{}>' # 구면좌표는 꺽쇠괄호를 이용하여 출력
else:
coords = self
outer_fmt = '({})' # 직교좌표는 괄호를 이용하여 출력
# 좌표의 각 항목을 요구사항에 따라 포맷하는 제너레이터 표현식 생성
components = (format(c, fmt_spec) for c in coords)
# 포맷된 요소들을 콤마로 분리하여 반환
return outer_fmt.format(', '.join(components))
@classmethod
def frombytes(cls, octets):
typecode = chr(octets[0])
memv = memoryview(octets[1:]).cast(typecode)
return cls(memv) # *를 이용해서 언패킹할 필요없음위의 포스팅에서 구현한 Vector 클래스에 시작하여 새로운 연산자를 몇 개 구현해보도록 하겠습니다. 이 클래스에는 이미 __abs__() 메소드는 구현되어 있으며, __neg__() 및 __pos__()를 연산자 메소드를 구현하면 다음과 같습니다.
class Vector:
# ... 나머지 메소드 생략
def __abs__(self):
# 파이썬 3.8부터 math.hypot은 n차원 포인트를 받을 수 있음, 파이썬 3.8 이전이라면
# math.sqrt(sum(x * x for x in self)) 로 작성
return math.hypot(*self)
def __neg__(self):
# -v를 계산하기 위해 새로운 Vector 객체를 만들고 self의 모든 요소를 반대값으로 채움
return Vector(-x for x in self)
def __pos__(self):
# +v를 계산하기 위해 새로운 Vector 객체를 만들고, self의 모든 요소로 채움
return Vector(self)
Vector 객체는 반복 가능하며, Vector.__init__()이 반복형 인수를 받기 때문에 __neg__()와 __pos__()는 위와 같이 짧게 구현할 수 있습니다. 여기서 __invert()__ 메소드는 구현하지 않을 것이므로 Vector 객체에 ~v 연산을 실행하면 파이썬은 단항 연산자 ~에 맞지 않는 피연산자라는 것을 의미하는 'bad operand type for unary ~: 'Vector'' 메세지와 함께 TypeError가 발생합니다.
x와 +x가 동일하지 않은 경우
일반적으로 x와 +x는 같을 것이라고 생각합니다(x == +x). 사실 파이썬에서는 거의 항상 똑같습니다. 그러나 표준 라이브러리 안에서 x와 +x가 다른 두 가지 케이스가 있습니다.
첫 번째 케이스는 decimal.Decimal 클래스와 관련되어 있습니다. 어떤 산술 컨텍스트(context)에서 Decimal 객체 x를 생성하고 나서 다르게 설정된 컨텍스트에서 +x를 평가하면 x와 +x가 달라질 수 있습니다.
예를 들어 x를 특정 정밀도로 계산하고 나서 정밀도를 변경한 후 +x를 평가하면 달라질 수 있습니다.
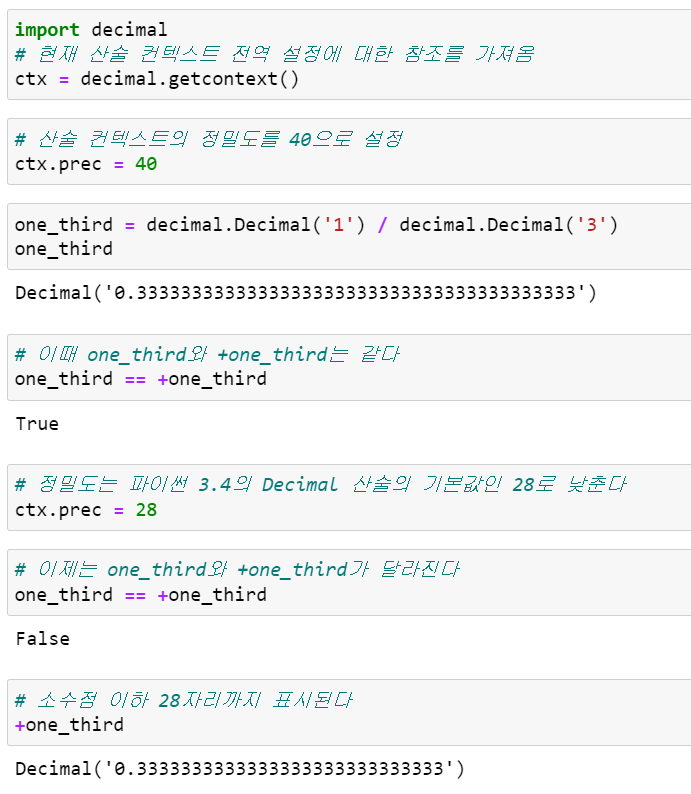
정리하면, +one_third 표현식이 나타날 때마다 one_third의 값을 이용해서 Decimal 객체를 새로 만드는데, 이때 현재의 산술 컨텍스트를 사용합니다.
x와 +x가 달라지는 두 번째 케이스는 collections.Counter 문서(link)에서 찾아볼 수 있습니다. Counter 클래스는 두 Counter 객체의 합계를 구하는 중위 연산자 + 등 여러 산술 연산자를 구현합니다. 그러나 실제로 카운터는 음수가 될 수 없으므로 Counter의 덧셈은 음수나 0인 카운터를 버립니다. 그리고 객체 앞에 붙은 +는 빈 Counter를 더하는 연산이므로 0보다 큰 값만 유지하는 Counter 객체를 새로 생성합니다. 예제를 살펴보겠습니다.

Overloading + for Vector Addition
벡터 두 개를 더하면 양쪽 베터 각 요소의 합으로 구성된 새로운 벡터가 생성됩니다. 다음 예제를 살펴보겠습니다.

길이가 다른 두 개의 Vector 객체를 더하면 어떻게 될까요? 에러를 발생시킬 수도 있지만 정보 검색 등에서 활용되는 사례를 보면, 짧은 쪽 벡터의 빈 공간을 0으로 채워서 더하는 것이 낫습니다. 즉, 다음과 같이 동작해야 합니다.

이러한 요구사항을 기반으로 다음과 같이 __add__() 메소드를 간단하게 구현할 수 있습니다.
class Vector:
# ... 나머지 메소드 생략
def __add__(self, other):
# pairs는 self에서 a를, other에서 b를 가져와서 (a, b)를 생성하는 제너레이터
# self와 other의 길이가 다른 경우에는 짧은 쪽의 빠진 값들을 fillvalue로 채운다
pairs = itertools.zip_longest(self, other, fillvalue=0.0)
# pairs 양쪽 항목의 합을 생성하는 제너레이터 표현식을 이용해서 새로운 Vector 생성
return Vector(a + b for a, b in pairs)__add__() 메소드는 새로운 Vector 객체를 만들며, self나 other의 값을 변경하지 않습니다.
또한 아래 예제 코드에서 확인할 수 있는 것처럼, 위와 같이 구현한 Vector를 사용하면 Vector 객체를 Vector2d 객체나 튜플, 그리고 숫자를 생성하는 어떠한 반복형에도 더할 수 있습니다.

__add__() 메소드가 어떠한 반복형 객체라도 사용할 수 있는 zip_longest() 함수를 사용하며, zip_longest()가 생성한 pair의 합을 생성하는 (a + b) 제너레이터 표현식을 이용하여 새로운 Vector를 생성하기 때문에, 위의 예시처럼 Vector 객체와 다양한 반복형을 더할 수 있습니다.
하지만, 다음과 같이 피연산자의 순서를 바꾸면 덧셈 연산은 실패합니다.

서로 다른 객체형에 대한 연산을 지원하기 위해 파이썬은 중위 연산자의 스페셜 메소드에 스페셜 디스패치 메커니즘을 구현합니다. 파이썬은 a + b 표현식을 다음과 같은 절차에 따라 처리합니다.
- a에 __add__() 메소드가 정의되어 있으면, a.__add__(b)를 호출하고, 결과가 NotImplemented가 아니면 반환한다.
- a에 __add__() 메소드가 정의되어 있지 않거나, 정의되어 있더라도 호출 후 NotImplemented가 반환되면, b에 __radd__() 메소드가 정의되어 있는지 확인해서 b.__radd__(a)를 호출하고, 결과가 NotImplemented가 아니면 반환한다.
- b에 __radd__() 메소드가 정의되어 있지 않거나, 정의되어 있더라도 호출 후 NotImplemented가 반환되면, unsupported operand types 메세지와 함께 TypeError가 발생한다.

__radd__() 메소드는 __add__() 메소드의 'reflected' 또는 'reverse' 버전입니다. r을 역순(reversed)이라는 의미로 생각할 수도 있고, 오른쪽 피연산자의 메소드를 호출하므로 오른쪽(righthand)이라고 생각할 수도 있습니다. 어쨋든 __radd__(), __rsub__() 등의 메소드에서 'r'이 나타내는 것은 이러한 의미입니다.
따라서 이러한 덧셈을 제대로 실행하려면 Vector.__radd__() 메소드를 구현해야 합니다. 왼쪽 피연산자가 __add__()를 구현하고 있지 않거나, 구현하더라도 오른쪽 피연산자라를 처리할 수 없어서 NotImplemented를 반환할 때, 파이썬 인터프리터는 최후의 수단으로 오른쪽 연산자의 __radd__() 메소드를 호출합니다.
NotImplemented와 NotImplementedError를 혼동하지 않아야 합니다. NotImplemented는 중위 연산자가 주어진 피연산자를 처리할 수 없을 때 파이썬 인터프리터에 '반환'하는 특별한 싱글턴 값입니다. 반면 NotImplementedError는 서브클래스에서 반드시 오버라이드해야 함을 알려주기 위해 추상 클래스의 메소드 stub에서 발생시키는 예외입니다.
__radd__()를 가장 간단하게 구현하는 방법은 다음과 같습니다.
class Vector:
# ... 나머지 메소드 생략
def __add__(self, other):
# pairs는 self에서 a를, other에서 b를 가져와서 (a, b)를 생성하는 제너레이터
# self와 other의 길이가 다른 경우에는 짧은 쪽의 빠진 값들을 fillvalue로 채운다
pairs = itertools.zip_longest(self, other, fillvalue=0.0)
# pairs 양쪽 항목의 합을 생성하는 제너레이터 표현식을 이용해서 새로운 Vector 생성
return Vector(a + b for a, b in pairs)
def __radd__(self, other):
# 단지 __add__() 메소드에 처리를 위임한다
return self + other__radd__() 메소드는 종종 이렇게 간단하게 구현됩니다. 단지 적절한 연산자를 호출하면 됩니다. 이런 방식은 교환 법칙이 성립하는 모든 연산자에 적용할 수 있씁니다. 숫자나 여기서 구현한 Vector 클래스의 경우 + 연산자의 교환 법칙이 성립하지만, 파이썬에서 시퀀스를 연결할 때의 + 연산자는 교환 법칙이 성립하지 않습니다.
이렇게 __radd__()를 구현하면 Vector 객체나 Vector2d, 정수들의 튜플, 실수들의 배열 등 숫자 항목으로 구성된 어떠한 반복형에도 사용할 수 있습니다. 그러나 비반복형 객체에 적용하면 __add__()는 다음과 같이 에러가 발생합니다.
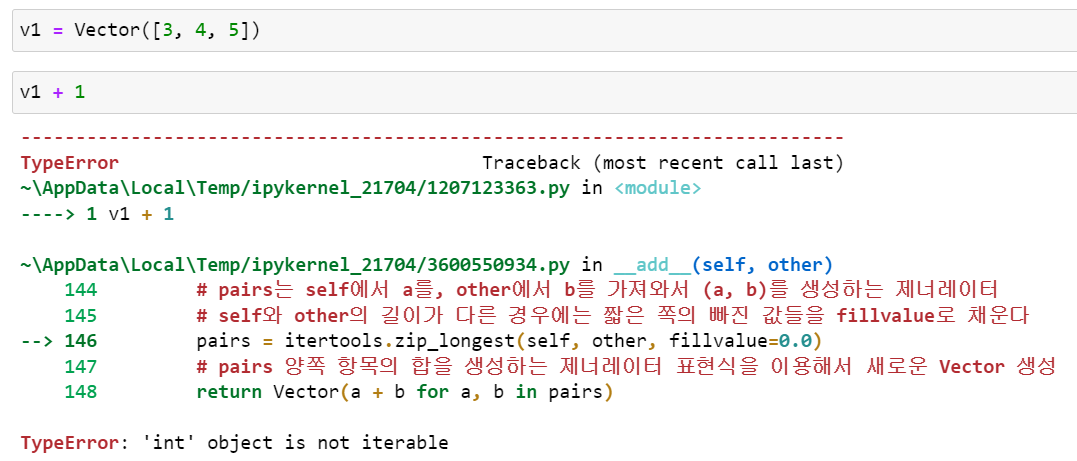
피연산자가 반복형이지만, 이 반복형 안의 항목과 Vector 안의 실수형 항목이 덧셈 연산을 수행할 수 없을 때는 다음과 같은 에러가 발생합니다.

이러한 에러 메세지보다 더 심각한 문제가 있습니다. 연산자 스페셜 메소드가 자료형의 비호환성 문제 때문에 적절한 결과를 반환할 수 없을 때는 NotImplemented 값을 반환해야지 TypeError 예외를 발생시키면 안됩니다. NotImplemented를 반환함으로써 파이썬이 reverse(righthand) 메소드를 호출하려고 시도할 때 다른 피연산자 자료형의 구현자에 연산을 처리할 수 있는 기회를 줄 수 있기 때문입니다.
덕 타이핑에서는 other 피연산자의 자료형이나 그 안에 들어 있는 요소의 자료형을 검사하지 않습니다. 대신 예외를 잡은 후 NotImplemented를 반환합니다. 이때 아직 파이썬 인터프리터가 reverse 연산을 시도하지 않았다면 reverse 연산을 시도합니다. reverse 연산 호출이 NotImplemented를 반환하면 그때서야 파이썬 인터프리터가 'unsupported operand type(s) for +: Vector and str.' 등의 표준 에러 메세지와 함께 TypeError를 발생시킵니다.
이러한 문제점을 고려하여 구현한 최종 버전의 __add__()와 __radd__()는 다음과 같습니다.
class Vector:
# ... 나머지 메소드 생략
def __add__(self, other):
try:
# pairs는 self에서 a를, other에서 b를 가져와서 (a, b)를 생성하는 제너레이터
# self와 other의 길이가 다른 경우에는 짧은 쪽의 빠진 값들을 fillvalue로 채운다
pairs = itertools.zip_longest(self, other, fillvalue=0.0)
# pairs 양쪽 항목의 합을 생성하는 제너레이터 표현식을 이용해서 새로운 Vector 생성
return Vector(a + b for a, b in pairs)
except TypeError:
return NotImplemented
def __radd__(self, other):
# 단지 __add__() 메소드에 처리를 위임한다
return self + other
Overloading * for Scalar Multiplication
Vector([1, 2, 3]) * x의 의미는 무엇일까요? x가 숫자라면 이 문장은 스칼라곱으로써, 벡터의 각 항목에 x를 곱해서 새로운 Vector 객체를 생성하는 것을 뜻합니다.

Vector 피연산자를 이용하는 다른 종류의 곱셈은 두 벡터의 내적을 구하는 것입니다. 현재 Numpy 및 이와 유사한 라이브러리에서는 * 연산자를 사용하는 경우, 벡터의 각 항목에 값을 곱하며, 벡터의 스칼라곱을 구하기 위해서는 numpy.dot() 함수를 사용합니다.
다시 벡터와 스칼라곱으로 돌아와서, 먼저 동작하는 가장 간단한 __mul__()과 __rmul__() 메소드를 구현해보겠습니다.
class Vector:
# ... 나머지 메소드 생략
def __mul__(self, scalar):
return Vector(n * scalar for n in self)
def __rmul__(self, scalar):
return self * scalar이 메소드들은 호환되는 피연산자들을 사용하는 한 제대로 동작합니다. scalar 인수는 float형을 곱했을 때 float형 결과가 나오는 숫자이어야 합니다(Vector 클래스가 내부적으로 float 배열을 사용하기 때문). 따라서 complex를 사용할 수는 없지만, int, bool, 심지어 fractions.Fraction 객체도 사용할 수 있습니다.
아래에서 구현한 __mul__()은 덧셈 연산자를 구현한 것처럼 scalar에 대해 명시적인 타입 검사는 하지 않지만, 대신 float 타입으로 변환하고 만약 변환이 실패한다면 NotImplemented를 반환하도록 합니다. 이는 덕 타이핑의 또 다른 예 입니다.
class Vector:
# ... 나머지 메소드 생략
def __mul__(self, scalar):
try:
factor = float(scalar)
except TypeError: # 스칼라가 float로 변환되지 않는다면
return NotImplemented # NotImplemented 반환
return Vector(n * factor for n in self)
def __rmul__(self, scalar):
return self * scalar이렇게 구현한 클래스를 이용하면 일반적인 수치형뿐만 아니라 보기 드문 수치형의 스칼라 값으로도 Vector 객체를 곱할 수 있습니다.

Using @ as an infix operator
이제 Vector간의 곱셈을 구현하는 방법에 대해 살펴보겠습니다. '@' 기호는 함수 데코레이터의 prefix로 잘 알려져 있지만, 2015년부터 이는 중위(infix) 연산자로도 사용될 수 있습니다. Numpy에서는 내적(dot product) 연산은 numpy.dot(a, b)와 같이 작성되었습니다. 이러한 함수 호출 표기법은 더 긴 공식을 수학 표기법에서 파이썬으로 변환하기 어렵게 만듭니다. 그래서 수치 컴퓨팅 커뮤니티는 파이썬 3.5에서 구현된 PEP 465를 위해서 로비하였습니다. 이제 두 Numpy 배열의 내적 연산은 a @ b처럼 작성할 수 있습니다.
@ 연산자는 __matmul__(), __rmatmul__(), __imatmul__() 이라는 스페셜 메소드에 의해 지원되며, 이들은 'matrix multiplication'이라고 불립니다. 이 메소드들은 파이썬 3.5 이후의 인터프리터에서 인식됩니다.
Vector 인스턴스에 @ 연산자의 동작은 다음과 같이 테스트됩니다.
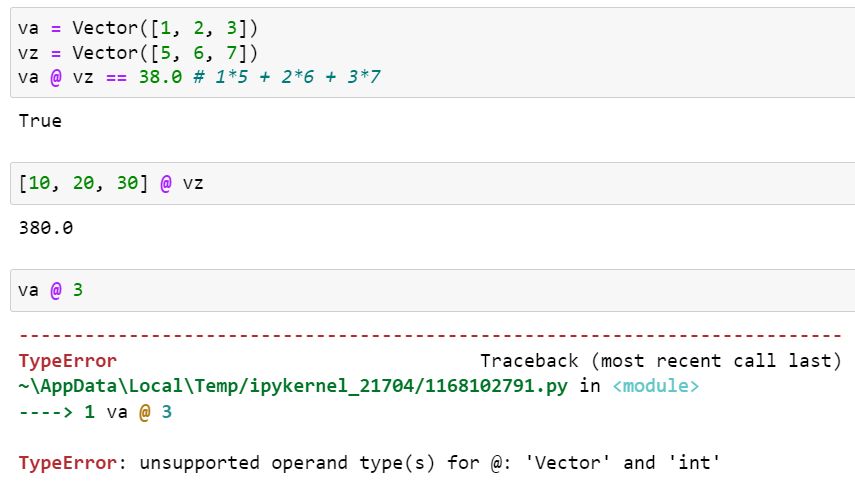
이렇게 동작하기 위해서 __matmul__()과 __rmatmul__()은 다음과 같이 구현됩니다.
from array import array
import reprlib
import math
import operator
import functools
import itertools
from collections import abc
class Vector:
# ... 나머지 메소드 생략
def __matmul__(self, other):
# 두 피연산자는 모두 __len__()과 __iter__()를 구현해야함
if (isinstance(other, abc.Sized) and
isinstance(other, abc.Iterable)):
if len(self) == len(other):
# 길이가 같을 때 sum, zip, 제너레이터 표현식으로 내적 계산
return sum(a * b for a, b in zip(self, other))
else:
raise ValueError('@ reuiqres vectors of equal length.')
else:
return NotImplemented
def __rmatmul__(self, other):
return self @ other위 코드는 구스 타이핑의 좋은 예시입니다. 여기서 other 피연산자를 Vector에 대해 테스트했다면, @ 연산자에 리스트나 배열을 사용하는 유연성이 없어질 것입니다. 한 피연산자가 Vector인 한, 우리가 구현한 @은 abc.Sized와 abc.Iterable의 인스턴스인 다른 모든 피연산자를 지원합니다. 두 ABCs는 __subclasshook__을 구현합니다. 따라서 __len__()과 __iter__()를 제공하는 어떠한 객체는 이들을 상속하지 않아도 테스트를 통과합니다. 특히 Vector 클래스는 abc.Sized나 abc.Iterable을 상속하지 않지만, 이들이 요구하는 필요한 메소드들을 가지고 있기 때문에 ABCs에 대한 isinstance 테스트를 통과합니다.
Wrapping-up arithmetic operators
+와 *, 그리고 @ 연산자를 구현하면서 중위 연산자를 구현하는 일반적인 패턴을 살펴봤습니다. 위에서 설명한 기법들은 아래 표에 나열된 모든 연산자에 적용할 수 있습니다.

Rich Comparision Operators
파이썬 인터프리터가 ==, !=, >, <, >=, <= 비교 연산자를 다루는 방법은 앞서 설명한 방법과 비슷하지만, 다음과 같은 중요한 차이점들이 있습니다.
- 아래 표에서 나열한 것처럼 정방향(forward method call)과 역방향(reverse method call)에 동일한 세트의 메소드가 사용됩니다. 예를 들어, == 연산자의 경우에는 forward와 reverse call에 동일한 __eq__() 메소드를 호출하지만, 정방향으로 __gt__() 메소드를 호출하는 경우, 역순으로는 인수를 바꿔서 __lt__() 메소드를 호출합니다.
- ==와 != 연산자의 경우 reverse 메소드가 실패하면, 파이썬은 TypeError를 발생시키는 대신 객체의 ID를 비교합니다.

모든 비교 연산자의 fallback step은 파이썬 2와 달라졌습니다. __ne__()의 경우, 파이썬3에서는 단지 __eq__()의 반댓값이 반환됩니다. 순서 비교 연산자의 경우, 예를 들어 정수와 튜플을 비교하면 파이썬 3에서는 'unordered types: int() < tuple()'과 같은 메세지와 함께 TypeError가 발생하지만, 파이썬 2에서 이러한 비교는 객체의 ID를 이용해서 임의적으로 비교한 이상한 결과가 나왔습니다. 사실 정수와 튜플을 비교하는 것은 의미가 없으므로 파이썬 3에서 제대로 개선되었다고 볼 수 있습니다.
지금까지 설명한 규칙에 따라 Vector 클래스에 다음고 같이 구현되어 있는 __eq__() 메소드의 동작을 개선해보도록 하겠습니다.
class Vector:
# ... 나머지 메소드 생략
def __eq__(self, other):
return (len(self) == len(other) and
all(a == b for a, b in zip(self, other)))이 메소드는 다음과 같이 실행됩니다.

경우에 따라 마지막 문장은 바람직하지 않을 수 있습니다. 이에 대한 엄격한 규칙은 없으면, 어플리케이션에 따라 다릅니다. 하지만 피연산자를 평가할 때 지나친 자유분방함은 예기치 못한 결과를 낳을 수 있으며 문제가 될 수 있습니다.
파이썬 자체를 보면 [1, 2] == (1, 2)는 거짓입니다. 그러므로 보수적인 입장을 취하고 어느 정도 자료형을 검사하도록 변경해보겠습니다. 두 번째 피연산자가 Vector나 Vector의 서브클래스의 객체인지 검사하고, 그렇다면 기존 __eq__() 메소드와 동일하게 처리합니다. 그렇지 않은 경우에는 NotImplemented를 반환해서 파이썬 인터프리터가 처리할 수 있게 해줍니다.
class Vector:
# ... 나머지 메소드 생략
def __eq__(self, other):
# other 피연산자가 Vector나 Vector의 서브클래스의 객체면 기존과 동일하게 비교
if isinstance(other, Vector):
return (len(self) == len(other) and
all(a == b for a, b in zip(self, other)))
else:
# 그렇지 않으면 NotImplemented 반환
return NotImplemented이렇게 구현한 Vector.__eq__() 메소드로 위와 동일한 테스트를 한 결과는 다음과 같습니다.

위의 테스트 중 첫 번째는 당연한 결과이지만, 나머지 두 개는 NotImplemented를 반환하는 __eq__() 메소드 때문에 위와 같은 결과가 나옵니다. 먼저 Vector와 Vector2d 객체에 일어난 동작을 단계별로 살펴보면 다음과 같습니다.
- vc == v2d를 평가하기 위해 파이썬은 Vector.__eq__(vc, v2d)를 호출
- Vector.__eq__(vc, v2d)는 v2d가 Vector 객체가 아님을 확인하고 NotImplemented를 반환
- NotImplemented가 반환되었으므로 파이썬은 Vector2d.__eq__(v2d, vc)를 실행
- Vector2d.__eq__(v2d, vc)는 피연산자 두 개를 모두 튜플로 변환해서 비교한다. 따라서 결과가 True가 된다.
위의 테스트에서 Vector와 tuple의 비교는 다음과 같은 단계로 처리됩니다.
- va == t3를 평가하기 위해서 파이썬 인터프리터가 Vector.__eq__(va, t3)를 호출
- Vector.__eq__(va, t3)은 t3가 Vector 타입이 아닌지 검사하고 NotImplemented를 반환
- NotImplemented를 받은 파이썬 인터프리터는 tuple.__eq__(t3, va)를 시도
- tuple.__eq__(t3, va)는 Vector 타입에 대해 알지 못하므로 NotImplemented를 반환
- == 연산자의 경우 특별히 reverse 메소드가 NotImplemented를 반환하면, 파이썬 인터프리터는 최후의 수단으로 두 객체의 ID를 비교한다
!= 연산자는 어떻게 해야 할까요 ? object로부터 상속받은 __ne__() 메소드가 최후에 호출되면서 우리 목적에 맞게 처리해주므로, 직접 구현할 필요는 없습니다. __eq__() 메소드가 구현되어 있고 NotImplemented를 반환하지 않으면, __ne__()는 __eq__()가 반환한 값의 반댓값을 반환합니다.
즉, 위의 테스트에서 사용한 객체들에 대한 != 연산자는 다음과 같이 일관된 결과를 반환합니다.

object 클래스에서 상속한 __ne__() 메소드는 원본이 C 언어로 구현되어 있다는 점을 제외하고는 다음 코드와 동일하게 동작합니다.
def __ne__(self, other):
eq_result = self == other
if eq_result is NotImplemented:
return NotImplemented
else:
return not eq_result
Augmented Assignmnet Operators
지금까지 구현한 Vector 클래스는 이미 +=와 *= 복합 할당 연산자(Augmented Assignment Operator)를 지원하고 있습니다. 아래 예제 코드에서 이를 확인해보도록 하겠습니다.

클래스가 in-place 연산자(ex, __iadd__(), __isub__() 등)을 구현하지 않으면, 복합 할당 연산자는 단지 편의 구문으로서, a += b를 a = a + b와 동일하게 평가합니다. 가변형의 경우 이렇게 동작하는 것이 타당하고, __add__() 메소드가 구현되어 있으면 아무런 코드를 추가하지 않고도 += 연산자가 작동합니다.
그러나 __iadd__() 등의 in-place 연산자 메소드를 정의한 경우, a += b를 계산하기 위해 정의된 메소드가 호출됩니다. 이름에서도 알 수 있듯이 이런 연산자는 새로운 객체를 생성하지 않고 왼쪽에 나온 피연산자를 직접 변경합니다.
in-place 연산자처럼 피연산자를 변경하는 스페셜 메소드는 여기서 구현한 Vector 클래스와 같은 불변 자료형에서는 당연히 구현하면 안됩니다.
객체의 내용을 변경하는 연산자를 보여주기 위해서 아래의 BingoCage 클래스를 확장하여 __add__()와 __iadd__()를 구현해보겠습니다.
# tombola.py
import abc
# ABC를 정의하려면 abc.ABC를 상속해야 한다.
class Tombola(abc.ABC):
# 추상 메소드를 @abstractmethod 데코레이터로 표시한다.
# 이 데코레이터에는 docstring만 들어 있는 경우가 종종 있다.
@abc.abstractmethod
def load(self, iterable):
"""Add items from an iterable."""
# 골라낼 항목이 없는 경우 LookupError를 발생시키라고 doctstring을 통해 구현자에게 알려줌
@abc.abstractmethod
def pick(self):
"""Remove item at random, returning it.
This method should raise `LookupError` when the instance is empty."""
# ABC에도 구상 메소드가 들어갈 수 있음
def loaded(self):
"""Return `True` if there's at least 1 item, `False` otherwise."""
# ABC의 구상 메소드는 반드시 ABC에 정의된 인터페이스만 사용해야 함
return bool(self.inspect())
def inspect(self):
"""Return a sorted tuple with the items currently inside."""
items = []
# 구상 서브클래스가 항목을 저장하는 방법은 알 수 없지만, pick()을 계속 호출해서
# Tombola 객체를 비움으로써 inspect()가 제공해야 하는 결과를 만들 수 있음
while True:
try:
items.append(self.pick())
except LookupError:
break
# load()를 호출해서 다시 넣어줌
self.load(items)
return tuple(items)# bingo.py
import random
from tombola import Tombola
# BingoCage 클래스는 Tombola를 명시적으로 상속함
class BingoCage(Tombola):
def __init__(self, items):
# random.SystemRandom 클래스는 os.urandom() 함수를 기반으로 random API를 구현
self._randomizer = random.SystemRandom()
self._items = []
# 초기화 작업을 load() 메소드에 위임
self.load(items)
def load(self, items):
self._items.extend(items)
# 평범한 random.shuffle() 대신 SystemRandom 객체의 shuffle() 메소드를 사용
self._randomizer.shuffle(self._items)
def pick(self):
try:
return self._items.pop()
except IndexError:
raise LookupError('pick from empty BingoCage')
# Tombola 인터페이스를 만족시키기 위해 필요한 것은 아님
def __call__(self):
self.pick()위 클래스들은 아래 포스팅에서 살펴봤던 클래스입니다.
[Python] Interfaces, Protocols, and ABCs
새로운 서브클래스 AddableBingoCage는 다음과 같이 구현할 수 있습니다.
from tombola import Tombola
from bingo import BingoCage
# AddableBingoCage는 BingoCage를 확장함
class AddableBingoCage(BingoCage):
def __add__(self, other):
# __add__() 메소드는 두 번째 피연산자가 Tombola 객체일 때만 동작함
if isinstance(other, Tombola):
return AddableBingoCage(self.inspect() + other.inspect())
else:
return NotImplemented
def __iadd__(self, other):
if isinstance(other, Tombola):
# other이 Tombola의 인스턴스라면 other의 항목들을 탐색
other_iterable = other.inspect()
else:
try:
# Tombola의 인스턴스가 아니라면 other의 iterator를 가져옴
other_iterable = iter(other)
except TypeError:
# 실패하면 메세지와 함게 에러를 발생
self_cls = type(self).__name__
msg = "right operand in += must be {!r} or an iterable"
raise TypeError(msg.format(self_cls))
# 여기까지 도달하면 other_iterable을 self에 로딩
self.load(other_iterable)
return self # 복합 할당 연산자는 반드시 self를 반환해야함__add__()와 __iadd__() 메소드를 구현하여 확장한 새로운 서브클래스 AddableBingoCage는 다음과 같은 + 연산자의 동작을 보여줍니다.
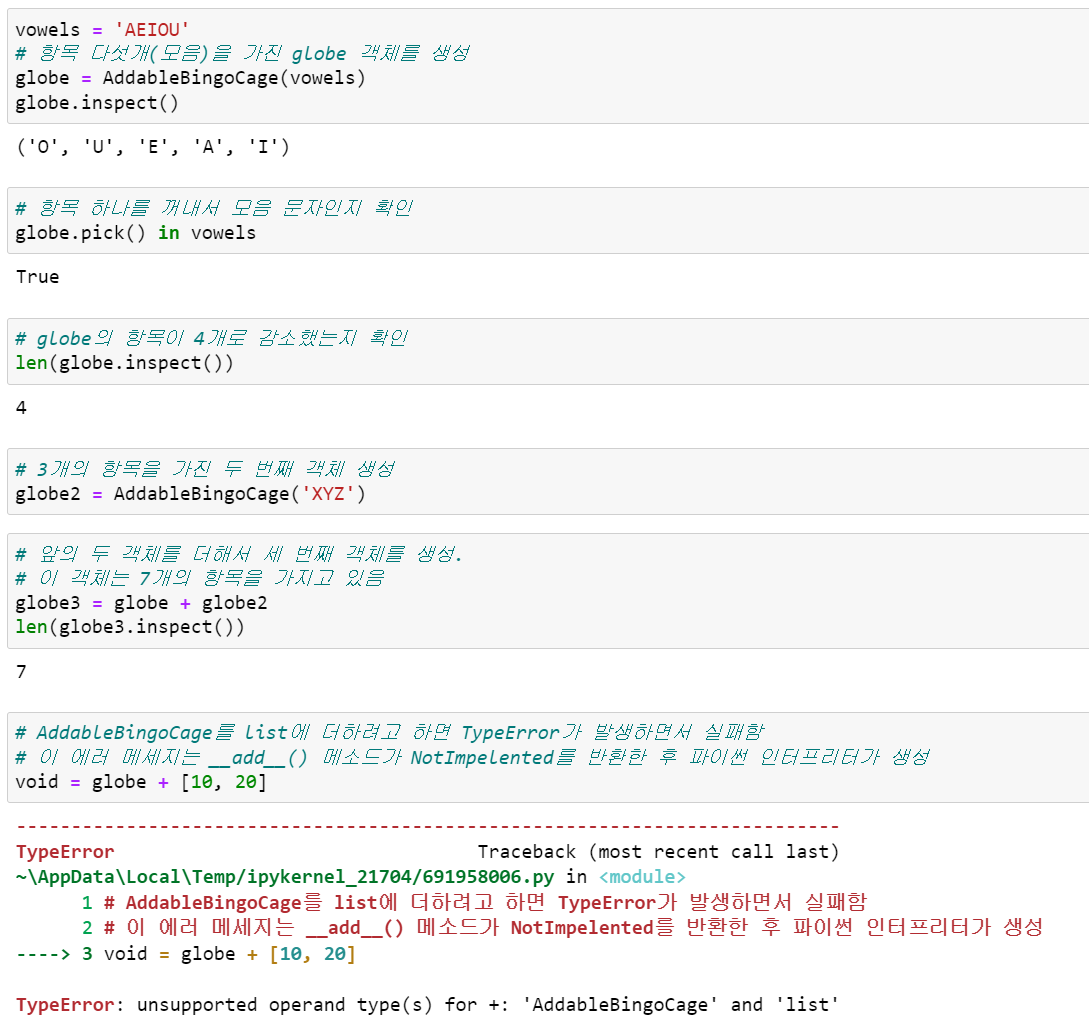
AddableBingoCage는 가변형이므로 다음 예제 코드에서 __iadd__()를 직접 구현했을 때 어떻게 동작하는지 보여줍니다.

두 번째 피연산자 측면에서 살펴보면 += 연산자가 + 연산자보다 자유롭습니다. + 연산자의 경우 서로 다른 자료형을 받으면 결과가 어떤 자료형이 되어야 하는지 혼란스러울 수 있으므로, 양쪽 피연산자가 동일한 자료형(여기서는 AddableBingoCage)이기를 원합니다. += 연산자의 경우에는 이러한 혼란이 없습니다. 왼쪽 객체의 내용이 갱신되므로, 연산 결과 자료형이 명확합니다.
AddableBingoCage 클래스에서 __add__()와 __iadd__() 메소드에서 결과를 생성하는 return문을 비교해서 in-place 연산자의 특징을 다음과 같이 정리할 수 있습니다.
- __add__() : AddableBingoCage()를 호출해서 생성된 새로운 객체를 반환
- __iadd__() : 객체 자신을 변경한 후 self를 반환
구조적으로 AddableBingoCage에는 __radd__()가 구현되어 있지 않습니다. 이는 이 메소드가 필요없기 때문입니다. 정방향 메소드 __add__()는 오른쪽에도 동일한 자료형이 와야 작동하므로, AddableBingoCage인 a와 AddableBingoCage가 아닌 b를 이용해서 파이썬이 a + b를 계산하면 NotImplemented를 반환하므로 b 객체의 클래스가 이 연산을 처리할 수 있습니다. 그러나 표현식이 b + a이고, b가 AddableBingoCage가 아니며 NotImplemented를 리턴한다면 파이썬이 b 객체를 처리할 수 없기 때문에 TypeError를 발생시키고 포기하는 것이 낫습니다.
'프로그래밍 > Python' 카테고리의 다른 글
| [Python] Context Mangers and else Blocks (0) | 2022.03.26 |
|---|---|
| [Python] Iterables, Iterators, and Generators (0) | 2022.03.25 |
| [Python] Interfaces, Protocols, and ABCs (2) | 2022.03.23 |
| [Python] Special Methods for Sequences (0) | 2022.03.21 |
| [Python] Data Class Builders (0) | 2022.03.20 |




댓글