해당 내용은 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 다섯 번째 강의 Recurrent Neural Network를 듣고 정리한 내용입니다. (Week 2)
2주차 첫번째 실습은 Word Embedding의 bias를 제거하는 방법을 직접 구현해보는 것입니다.
임베딩은 미리 학습된 GloVe 임베딩을 사용할 것이며, 이는 nlp.stanford.edu/projects/glove/ 에서 다운받을 수 있습니다.
import numpy as np def read_glove_vecs(glove_file): with open(glove_file, 'r', encoding='utf-8') as f: words = set() word_to_vec_map = {} for line in f: line = line.strip().split() curr_word = line[0] words.add(curr_word) word_to_vec_map[curr_word] = np.array(line[1:], dtype=np.float64) return words, word_to_vec_map
위 함수는 미리 학습된 임베딩 파일을 읽어서, 각 단어의 벡터를 반환하는 함수입니다.
words는 vocabulary에 있는 단어 set이며, word_to_vec_map는 단어와 그 단어의 벡터를 매핑하는 딕셔너리입니다.
words, word_to_vec_map = read_glove_vecs('./data/glove.6B.50d.txt') print(len(words)) print(word_to_vec_map['doctor'].shape) print(word_to_vec_map['doctor'])

사용되는 임베딩 파일은 60억개의 토큰으로 50 dimension을 갖는 임베딩 벡터를 사용합니다.
총 40만개의 단어가 있으며, 각 단어는 50차원의 벡터입니다.
one-hot vectors는 각 단어간의 유클리디안(Euclidean) 거리가 모두 동일하여 단어 간의 유사성을 비교할 수 없지만, 임베딩은 실수값을 갖는 벡터로 이루어지기 때문에 각 벡터는 개별 단어의 의미를 제공하며, 단어 간의 유사성을 포착하기에 더 유용합니다.
1. Cosine similarity
두 단어 간의 유사성을 측정하기 위해서, 두 단어의 임베딩 벡터의 유사성 정도를 측정하는 방법이 필요한데, 주로 Cosine similarily(코사인 유사성)가 많이 사용됩니다.
분자의 벡터 u, v는 내적으로 연산되며, 는 벡터 u의 norm을 의미합니다.
그리고 는 벡터 u와 v의 사이의 각도입니다.
Cosine Similarity의 의미는 다음과 같습니다.

두 단어가 유사할수록 두 벡터의 각도가 0에 가깝고, 유사하지 않다면 90에 가깝습니다.
다음은 두 벡터 사이의 cosing similarity를 계산하는 함수입니다.
def cosine_similarity(u, v): """ Cosine similarity reflects the degree of similarity between u and v Arguments: u -- a word vector of shape (n,) v -- a word vector of shape (n,) Returns: cosine_similarity -- the cosine similarity between u and v defined by the formula above. """ distance = 0.0 ### START CODE HERE ### # Compute the dot product between u and v (≈1 line) dot = u.dot(v) # Compute the L2 norm of u (≈1 line) norm_u = np.sqrt(np.sum(u*u)) # Compute the L2 norm of v (≈1 line) norm_v = np.sqrt(np.sum(v*v)) # Compute the cosine similarity defined by formula (1) (≈1 line) cosine_similarity = dot / (norm_u * norm_v) ### END CODE HERE ### return cosine_similarity
테스트코드
father = word_to_vec_map["father"] mother = word_to_vec_map["mother"] ball = word_to_vec_map["ball"] crocodile = word_to_vec_map["crocodile"] france = word_to_vec_map["france"] italy = word_to_vec_map["italy"] paris = word_to_vec_map["paris"] rome = word_to_vec_map["rome"] print("cosine_similarity(father, mother) = ", cosine_similarity(father, mother)) print("cosine_similarity(ball, crocodile) = ",cosine_similarity(ball, crocodile)) print("cosine_similarity(france - paris, rome - italy) = ",cosine_similarity(france - paris, rome - italy))

단어 간의 관계가 유사할수록 값이 1에 가까우며, france-paris와 rome-italy 같이 반대로 계산된 벡터들의 유사도는 각도가 180도에 가까워지면서 -1에 가까운 값을 보여주고 있습니다.
2. Word analogy task
단어 유추 task를 통해서 "a is to b as c is to _____"에서의 빈칸을 완성해보도록 하겠습니다.
빈칸의 들어올 단어 d는 임베딩 벡터 를 가지고 아래 식을 만족하게 됩니다.
여기서 우리는 와 의 유사도를 cosine similarity를 통해서 측정할 수 있습니다.
def complete_analogy(word_a, word_b, word_c, word_to_vec_map): """ Performs the word analogy task as explained above: a is to b as c is to ____. Arguments: word_a -- a word, string word_b -- a word, string word_c -- a word, string word_to_vec_map -- dictionary that maps words to their corresponding vectors. Returns: best_word -- the word such that v_b - v_a is close to v_best_word - v_c, as measured by cosine similarity """ # convert words to lowercase word_a, word_b, word_c = word_a.lower(), word_b.lower(), word_c.lower() ### START CODE HERE ### # Get the word embeddings e_a, e_b and e_c (≈1-3 lines) e_a, e_b, e_c = word_to_vec_map[word_a], word_to_vec_map[word_b], word_to_vec_map[word_c] ### END CODE HERE ### words = word_to_vec_map.keys() max_cosine_sim = -100 # Initialize max_cosine_sim to a large negative number best_word = None # Initialize best_word with None, it will help keep track of the word to output # to avoid best_word being one of the input words, skip the input words # place the input words in a set for faster searching than a list # We will re-use this set of input words inside the for-loop input_words_set = set([word_a, word_b, word_c]) # loop over the whole word vector set for w in words: # to avoid best_word being one of the input words, skip the input words if w in input_words_set: continue ### START CODE HERE ### # Compute cosine similarity between the vector (e_b - e_a) and the vector ((w's vector representation) - e_c) (≈1 line) cosine_sim = cosine_similarity(e_b - e_a, word_to_vec_map[w] - e_c) # If the cosine_sim is more than the max_cosine_sim seen so far, # then: set the new max_cosine_sim to the current cosine_sim and the best_word to the current word (≈3 lines) if cosine_sim > max_cosine_sim: max_cosine_sim = cosine_sim best_word = w ### END CODE HERE ### return best_word
코드를 보시면 아시겠지만, 단어 d에 모든 단어를 대입해서 가장 높은 유사도를 갖는 단어를 찾아서 리턴하게 됩니다.
테스트코드
triads_to_try = [('italy', 'italian', 'spain'), ('india', 'delhi', 'japan'), ('man', 'woman', 'boy'), ('small', 'smaller', 'large')] for triad in triads_to_try: print ('{} -> {} :: {} -> {}'.format( *triad, complete_analogy(*triad,word_to_vec_map)))

3. Debiasing word vectors
다음으로 우리는 단어 임베딩에 반영된 gender biases를 측정해보고, 이 bias를 감소시키도록 해보겠습니다.
먼저 GloVe 단어 임베딩에서 gender와 관련된 벡터 g를 계산해보도록 하겠습니다. man의 벡터와 woman의 벡터의 차이로 구할 수 있습니다.
벡터 g는 대략적인 'gender'의 특성으로 인코딩된 것으로 볼 수 있으며, 를 추가로 계산해서 이들의 평균으로 사용해도 좋습니다. 지금은 단순히 을 사용하는 것이 더 좋은 결과를 보이기 때문에 이것으로 사용합니다.
g = word_to_vec_map['woman'] - word_to_vec_map['man'] print(g)

사람 이름 벡터와 gender 벡터의 코사인 유사도를 측정해보도록 하겠습니다.
print ('List of names and their similarities with constructed vector:') # girls and boys name name_list = ['john', 'marie', 'sophie', 'ronaldo', 'priya', 'rahul', 'danielle', 'reza', 'katy', 'yasmin'] for w in name_list: print (w, cosine_similarity(word_to_vec_map[w], g))

여성 이름은 양의 코사인 유사도로 계산되고, 남성 이름은 음의 코사인 유사도로 계산되는 경향이 있습니다.
다른 단어로 확인해보도록 하겠습니다.
print('Other words and their similarities:') word_list = ['lipstick', 'guns', 'science', 'arts', 'literature', 'warrior','doctor', 'tree', 'receptionist', 'technology', 'fashion', 'teacher', 'engineer', 'pilot', 'computer', 'singer'] for w in word_list: print (w, cosine_similarity(word_to_vec_map[w], g))

결과를 보시면, 성 고정관념이 임베딩에 반영되어 있는 것을 볼 수 있습니다.
actor/actress 또는 grandmother/grandfather은 gender specific하지만 receptionist 또는 technology는 중성적인 단어이며 gender specific하지 않습니다.
'Man is to Computer Programmer as Woman is to Homemaker ? Debiasing Word Embeddings'라는 논문에서 사용하는 알고리즘을 통해서 이러한 bias를 제거해보도록 하겠습니다.
3.1 Neutralize bias for non-gender specific words
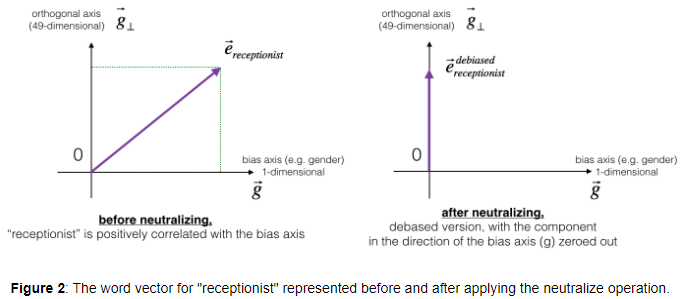
위 그래프는 중성화(neutralizing)이 하는 것이 무엇인지 보여주고 있습니다.
만약 50-dim의 단어 임베딩을 사용한다면, 50개의 차원은 bias-direction인 g vector와 g vector와 직교하는 나머지 49-dim vector 로 나누어집니다. 나머지 49-dim의 vector를 로 지칭하겠습니다.
선형대수학에서 는 g와 perpendicular(or 'orthogonal'), 즉 수직(직교) 관계입니다.
Nuetralizing step에서 에서 성분을 0으로 만들어주는 과정이 수행되고, 결과적으로 g vector의 방향 성분이 제거되어 가 됩니다.
debiasing은 아래와 같은 공식으로 제거할 수 있습니다.
\[\begin{matrix} e^{\text{bias\_component}} = \frac{e \cdot g}{\|g\|_2^2} \star g \\ e^{debiased} = e - e^{\text{bias\_component}} \end{matrix}\]
선형대수학 관점에서 는 vector e를 direction g에 정사영하는 것을 의미합니다.
def neutralize(word, g, word_to_vec_map): """ Removes the bias of "word" by projecting it on the space orthogonal to the bias axis. This function ensures that gender neutral words are zero in the gender subspace. Arguments: word -- string indicating the word to debias g -- numpy-array of shape (50,), corresponding to the bias axis (such as gender) word_to_vec_map -- dictionary mapping words to their corresponding vectors. Returns: e_debiased -- neutralized word vector representation of the input "word" """ ### START CODE HERE ### # Select word vector representation of "word". Use word_to_vec_map. (≈ 1 line) e = word_to_vec_map[word] # Compute e_biascomponent using the formula given above. (≈ 1 line) e_biascomponent = (e.dot(g)/np.sum(g*g)) * g # Neutralize e by subtracting e_biascomponent from it # e_debiased should be equal to its orthogonal projection. (≈ 1 line) e_debiased = e - e_biascomponent ### END CODE HERE ### return e_debiased
테스트코드
e = "receptionist" print("cosine similarity between " + e + " and g, before neutralizing: ", cosine_similarity(word_to_vec_map["receptionist"], g)) e_debiased = neutralize("receptionist", g, word_to_vec_map) print("cosine similarity between " + e + " and g, after neutralizing: ", cosine_similarity(e_debiased, g))
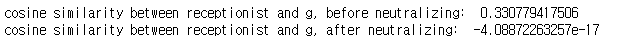
Neutralizing을 진행하여 gender vector g와 코사인 유사도가 거의 0이 된 것을 확인할 수 있습니다.
3.2 Equalization algorithm for gender-specific words
다음으로 actor/actress와 같이 gender-specific한 단어들을 equalization 해주는 작업이 필요합니다.
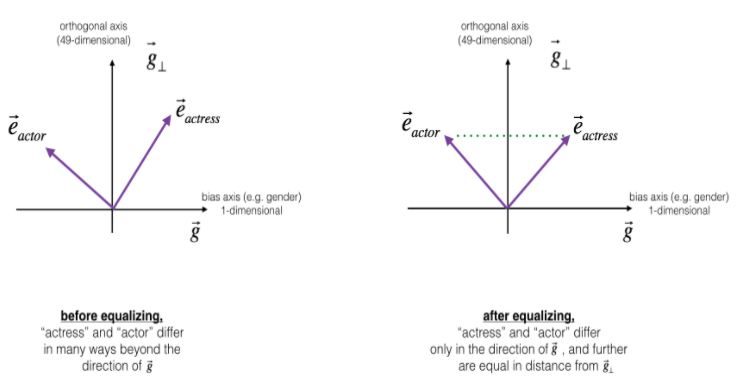
주요 아이디어는 특정 단어 쌍이 49-dim의 로부터의 거리가 같은지 확인하는 것입니다.
Equalizing step의 공식은 다음과 같습니다.

def equalize(pair, bias_axis, word_to_vec_map): """ Debias gender specific words by following the equalize method described in the figure above. Arguments: pair -- pair of strings of gender specific words to debias, e.g. ("actress", "actor") bias_axis -- numpy-array of shape (50,), vector corresponding to the bias axis, e.g. gender word_to_vec_map -- dictionary mapping words to their corresponding vectors Returns e_1 -- word vector corresponding to the first word e_2 -- word vector corresponding to the second word """ ### START CODE HERE ### # Step 1: Select word vector representation of "word". Use word_to_vec_map. (≈ 2 lines) w1, w2 = pair[0], pair[1] e_w1, e_w2 = word_to_vec_map[w1], word_to_vec_map[w2] # Step 2: Compute the mean of e_w1 and e_w2 (≈ 1 line) mu = (e_w1 + e_w2) / 2 # Step 3: Compute the projections of mu over the bias axis and the orthogonal axis (≈ 2 lines) mu_B = mu.dot(bias_axis)/np.sum(bias_axis*bias_axis) * bias_axis mu_orth = mu - mu_B # Step 4: Use equations (7) and (8) to compute e_w1B and e_w2B (≈2 lines) e_w1B = e_w1.dot(bias_axis)/np.sum(bias_axis*bias_axis) * bias_axis e_w2B = e_w2.dot(bias_axis)/np.sum(bias_axis*bias_axis) * bias_axis # Step 5: Adjust the Bias part of e_w1B and e_w2B using the formulas (9) and (10) given above (≈2 lines) corrected_e_w1B = np.sqrt(np.abs(1-np.sum(mu_orth*mu_orth))) * (e_w1B - mu_B) / np.sqrt(np.sum((e_w1 - mu_orth - mu_B)**2)) corrected_e_w2B = np.sqrt(np.abs(1-np.sum(mu_orth*mu_orth))) * (e_w2B - mu_B) / np.sqrt(np.sum((e_w2 - mu_orth - mu_B)**2)) # Step 6: Debias by equalizing e1 and e2 to the sum of their corrected projections (≈2 lines) e1 = corrected_e_w1B + mu_orth e2 = corrected_e_w2B + mu_orth ### END CODE HERE ### return e1, e2
테스트코드
print("cosine similarities before equalizing:") print("cosine_similarity(word_to_vec_map[\"man\"], gender) = ", cosine_similarity(word_to_vec_map["man"], g)) print("cosine_similarity(word_to_vec_map[\"woman\"], gender) = ", cosine_similarity(word_to_vec_map["woman"], g)) print() e1, e2 = equalize(("man", "woman"), g, word_to_vec_map) print("cosine similarities after equalizing:") print("cosine_similarity(e1, gender) = ", cosine_similarity(e1, g)) print("cosine_similarity(e2, gender) = ", cosine_similarity(e2, g))

두 벡터 e1, e2가 gender vector와의 거리 값이 동일해진 것을 확인할 수 있습니다.
'Coursera 강의 > Deep Learning' 카테고리의 다른 글
| [실습] Neural Machine Translation with Attention (0) | 2020.12.29 |
|---|---|
| Sequence models & Attention mechnism / Speech recognition(CTC) (0) | 2020.12.28 |
| NLP and Word Embeddings: Word2vec & GloVe (0) | 2020.12.26 |
| Introduction to Word Embeddings (0) | 2020.12.24 |
| [실습] Character-level Language Modeling (0) | 2020.12.21 |




댓글