해당 내용은 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 다섯 번째 강의 Recurrent Neural Network를 듣고 정리한 내용입니다. (Week 1)
RNN 1주차 실습은 Simple RNN, LSTM, GRU를 Step by step으로 구현해보는 것입니다. 그리고 다음 실습에서 이렇게 구현한 함수들을 통해서 Music generator를 구현해보도록 할 예정입니다.
실습에 들어가기 전에 Notation부터 설명하겠습니다.
- 위첨자 [l]은 layer를 의미함
- 위첨자 (i)는 sample data를 의미함
- 위첨자 <t>는 time-step을 의미함
- 아래첨자 i는 벡터의 요소를 의미함
- Example : 는 2번째 training example, 3번째 layer, 4번째 time-step, 5번째 요소를 의미함
import numpy as np from rnn_utils import *
필요한 패키지들을 import하고 실습 진행하도록 하겠습니다.
rnn_utils에는 softmax / sigmoid / initialize_adam / update_parameters_with_adam 함수가 내장되어 있습니다.
1. Forward propagation for the basic RNN
인 Basic RNN의 구조는 다음과 같습니다.

Simple RNN에서 입력과 출력으로 가 사용되는데, 각각의 dimension을 정리하고 구현해보도록 하겠습니다.
- Dimensions of Input x
Input x는 ()의 dimension을 가집니다.
- : number of units
Single time-step에서 하나의 input example 는 1차원 벡터인데, 이 1차원 벡터는 모델에서 사용되는 단어의 개수로 one-hot encoding됩니다. 만약 5000개의 단어를 사용한다면, 이 벡터()의 차원은 (5000, )이 됩니다.
- : time-step of size
- : Batches of size - mini-batch의 크기를 의미합니다.
- Dimensions of hidden state
Input tensor x와 유사하게, ()의 dimension을 갖습니다.
- Dimensions of prediction
위 두 차원과 유사하게 ()의 dimension을 갖습니다.
1.1 RNN cell
Basic RNN cell은 다음과 같으며, 하나의 cell에서 하나의 time-step이 연산됩니다.

따라서, RNN cell 연산의 결과로 각 time-step의 hidden state , prediction 를 반환합니다.

def rnn_cell_forward(xt, a_prev, parameters): """ Implements a single forward step of the RNN-cell as described in Figure (2) Arguments: xt -- your input data at timestep "t", numpy array of shape (n_x, m). a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m) parameters -- python dictionary containing: Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x) Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a) Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a) ba -- Bias, numpy array of shape (n_a, 1) by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1) Returns: a_next -- next hidden state, of shape (n_a, m) yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m) cache -- tuple of values needed for the backward pass, contains (a_next, a_prev, xt, parameters) """ # Retrieve parameters from "parameters" Wax = parameters["Wax"] Waa = parameters["Waa"] Wya = parameters["Wya"] ba = parameters["ba"] by = parameters["by"] ### START CODE HERE ### (≈2 lines) # compute next activation state using the formula given above a_next = np.tanh(Wax.dot(xt)+Waa.dot(a_prev)+ba) # compute output of the current cell using the formula given above yt_pred = softmax(Wya.dot(a_prev)+by) ### END CODE HERE ### # store values you need for backward propagation in cache cache = (a_next, a_prev, xt, parameters) return a_next, yt_pred, cache
테스트 코드입니다.
np.random.seed(1) xt_tmp = np.random.randn(3,10) a_prev_tmp = np.random.randn(5,10) parameters_tmp = {} parameters_tmp['Waa'] = np.random.randn(5,5) parameters_tmp['Wax'] = np.random.randn(5,3) parameters_tmp['Wya'] = np.random.randn(2,5) parameters_tmp['ba'] = np.random.randn(5,1) parameters_tmp['by'] = np.random.randn(2,1) a_next_tmp, yt_pred_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp) print("a_next[4] = \n", a_next_tmp[4]) print("a_next.shape = \n", a_next_tmp.shape) print("yt_pred[1] =\n", yt_pred_tmp[1]) print("yt_pred.shape = \n", yt_pred_tmp.shape)

1.2 RNN forward pass
RNN은 RNN cell들의 반복으로 구성됩니다. 만약 시퀀스 데이터의 길이가 10 time steps라면, RNN cell은 총 10번 호출되어 연산됩니다.

def rnn_forward(x, a0, parameters): """ Implement the forward propagation of the recurrent neural network described in Figure (3). Arguments: x -- Input data for every time-step, of shape (n_x, m, T_x). a0 -- Initial hidden state, of shape (n_a, m) parameters -- python dictionary containing: Waa -- Weight matrix multiplying the hidden state, numpy array of shape (n_a, n_a) Wax -- Weight matrix multiplying the input, numpy array of shape (n_a, n_x) Wya -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a) ba -- Bias numpy array of shape (n_a, 1) by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1) Returns: a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x) y_pred -- Predictions for every time-step, numpy array of shape (n_y, m, T_x) caches -- tuple of values needed for the backward pass, contains (list of caches, x) """ # Initialize "caches" which will contain the list of all caches caches = [] # Retrieve dimensions from shapes of x and parameters["Wya"] n_x, m, T_x = x.shape n_y, n_a = parameters["Wya"].shape ### START CODE HERE ### # initialize "a" and "y_pred" with zeros (≈2 lines) a = np.zeros((n_a, m, T_x)) y_pred = np.zeros((n_y, m, T_x)) # Initialize a_next (≈1 line) a_next = a0 # loop over all time-steps of the input 'x' (1 line) for t in range(T_x): # Update next hidden state, compute the prediction, get the cache (≈2 lines) xt = x[:,:,t] a_next, yt_pred, cache = rnn_cell_forward(xt, a_next, parameters) # Save the value of the new "next" hidden state in a (≈1 line) a[:,:,t] = a_next # Save the value of the prediction in y (≈1 line) y_pred[:,:,t] = yt_pred # Append "cache" to "caches" (≈1 line) caches.append(cache) ### END CODE HERE ### # store values needed for backward propagation in cache caches = (caches, x) return a, y_pred, caches
테스트 코드입니다.
np.random.seed(1) x_tmp = np.random.randn(3,10,4) a0_tmp = np.random.randn(5,10) parameters_tmp = {} parameters_tmp['Waa'] = np.random.randn(5,5) parameters_tmp['Wax'] = np.random.randn(5,3) parameters_tmp['Wya'] = np.random.randn(2,5) parameters_tmp['ba'] = np.random.randn(5,1) parameters_tmp['by'] = np.random.randn(2,1) a_tmp, y_pred_tmp, caches_tmp = rnn_forward(x_tmp, a0_tmp, parameters_tmp) print("a[4][1] = \n", a_tmp[4][1]) print("a.shape = \n", a_tmp.shape) print("y_pred[1][3] =\n", y_pred_tmp[1][3]) print("y_pred.shape = \n", y_pred_tmp.shape) print("caches[1][1][3] =\n", caches_tmp[1][1][3]) print("len(caches) = \n", len(caches_tmp))

여기까지가 Simple RNN의 forward propagation입니다.
하지만, Simple RNN은 vanishing gradient problem이 존재하며, Long Term Dependency 문제 또한 존재합니다. 따라서, Simple RNN은 Local Context에서 가장 좋은 성능을 나타냅니다.
(Local context는 가 t와 가까운 time-step의 input 에 의해서 예측되는 것을 의미합니다)
2. Long Short-Term Memory(LSTM) network
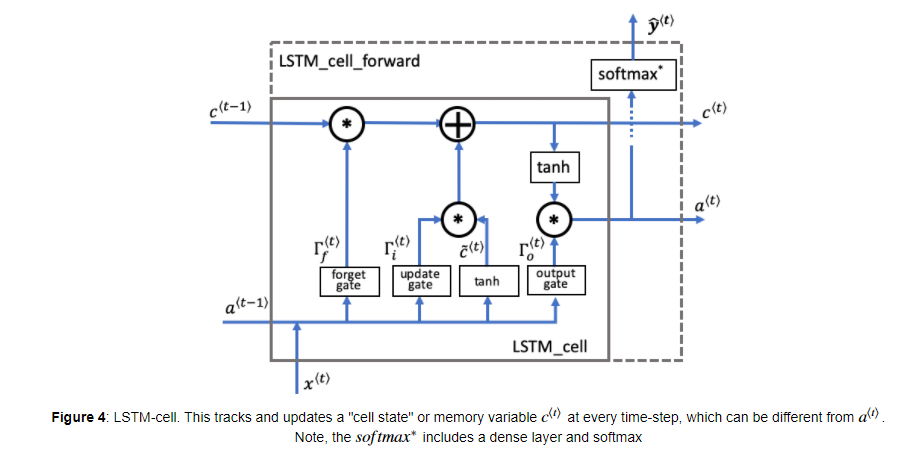
LSTM-cell의 구조는 위와 같습니다. Basic RNN 구조에서 매 time-step마다 장기 기억을 위한 가 input/output으로 추가되고, 내부에서 Candidate value , Forget gate , Update gate , Output gate 가 연산됩니다.
- Forget gate
Equation:
이전 time step의 결과 과 현재 time step의 input 는 concat을 통해서 합쳐진 후에 와 연산됩니다. 그리고 최종적으로 sigmoid 연산이 이루어지므로 결과는 0 ~ 1 사이의 값을 가지게 됩니다.
그 이후에 의 dimension은 와 동일하며, 과 곱연산(element-wise)이 수행됩니다.(이전 cell state에 masking 하는 것과 같습니다)
Forget gate는 그 이름처럼 이전 time step에서 저장된 정보를 다음 time step동안 유지할 지 결정합니다.
따라서, 가 0, or 0에 가깝다면 은 다음 time step에 기억되지 않고, 1에 가깝다면 를 다음 time step까지 유지하게 됩니다.
- Candidate value
Equation:
candidate value는 에 저장될 수 있는 현재 time step 단계의 정보(후보군)를 포함하는 Tensor입니다.
어떤 값이 전달되는 지는 Update gate에 따라서 다르며, tanh 함수가 적용되므로 -1 ~ 1의 값을 갖습니다.
(물결 표시는 current cell state인 와 후보군을 구분하기 위해 사용됩니다.)
- Update gate
Equation:
Update gate는 cell state에 추가할 candidate의 정보를 결정하는 역할을 합니다. 즉, candidate value 의 어떤 부분이 로 전다러되는지 결정하게 되며, 최종적으로 sigmoid 연산이 수행되므로 0 ~ 1 사이의 값을 갖습니다.
그래서 Upate gate의 값이 1에 가까우면, candidate 값이 hidden state 로 전달되도록 하고, 0에 가깝다면 cadidate value가 hidden state로 전달되지 않도록 합니다.
그리고 Update gate는 candidate value와 곱연산(element-wise)가 수행됩니다.
- Cell state
Equation:
Cell state는 다음 time step으로 전달되는 'memory'입니다. 이 값은 이전 cell state와 현재 candidate value의 결합으로 결정됩니다.
- Output gate
Equation:
Output gate는 현재 time step의 예측값으로 전달되는 대상을 결정합니다.
이전 hidden state 와 current input 에 의해서 값이 결정되며, sigmoid 함수가 마지막에 적용되므로 0 ~ 1 사이의 값을 갖습니다.
- Hidden state
Equation:
hidden state는 LSTM cell의 다음 time step에 전달되는 값을 얻으며, 동시에 예측값 를 구하기 위해서 사용됩니다.
Cell state의 값은 tanh에 의해서 -1 ~ 1 사이의 값으로 rescaling되며, Output gate는 이 값이 hidden state 에 포함될지 안될지를 결정하게 됩니다.
- Prediction
Equation:
2.1 LSTM cell

하나의 LSTM cell을 구현해보도록 하겠습니다. 이전 hidden state 와 현재 input 는 np.concatenate 함수를 통해서 쌓아줍니다.
def lstm_cell_forward(xt, a_prev, c_prev, parameters): """ Implement a single forward step of the LSTM-cell as described in Figure (4) Arguments: xt -- your input data at timestep "t", numpy array of shape (n_x, m). a_prev -- Hidden state at timestep "t-1", numpy array of shape (n_a, m) c_prev -- Memory state at timestep "t-1", numpy array of shape (n_a, m) parameters -- python dictionary containing: Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x) bf -- Bias of the forget gate, numpy array of shape (n_a, 1) Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x) bi -- Bias of the update gate, numpy array of shape (n_a, 1) Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x) bc -- Bias of the first "tanh", numpy array of shape (n_a, 1) Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x) bo -- Bias of the output gate, numpy array of shape (n_a, 1) Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a) by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1) Returns: a_next -- next hidden state, of shape (n_a, m) c_next -- next memory state, of shape (n_a, m) yt_pred -- prediction at timestep "t", numpy array of shape (n_y, m) cache -- tuple of values needed for the backward pass, contains (a_next, c_next, a_prev, c_prev, xt, parameters) Note: ft/it/ot stand for the forget/update/output gates, cct stands for the candidate value (c tilde), c stands for the cell state (memory) """ # Retrieve parameters from "parameters" Wf = parameters["Wf"] # forget gate weight bf = parameters["bf"] Wi = parameters["Wi"] # update gate weight (notice the variable name) bi = parameters["bi"] # (notice the variable name) Wc = parameters["Wc"] # candidate value weight bc = parameters["bc"] Wo = parameters["Wo"] # output gate weight bo = parameters["bo"] Wy = parameters["Wy"] # prediction weight by = parameters["by"] # Retrieve dimensions from shapes of xt and Wy n_x, m = xt.shape n_y, n_a = Wy.shape ### START CODE HERE ### # Concatenate a_prev and xt (≈1 line) concat = np.concatenate((a_prev, xt), axis=0) # Compute values for ft (forget gate), it (update gate), # cct (candidate value), c_next (cell state), # ot (output gate), a_next (hidden state) (≈6 lines) ft = sigmoid(Wf.dot(concat) + bf) # forget gate it = sigmoid(Wi.dot(concat) + bi) # update gate cct = np.tanh(Wc.dot(concat) + bc) # candidate value c_next = ft*c_prev + it*cct # cell state ot = sigmoid(Wo.dot(concat) + bo) # output gate a_next = ot*np.tanh(c_next) # hidden state # Compute prediction of the LSTM cell (≈1 line) yt_pred = softmax(Wy.dot(a_next) + by) ### END CODE HERE ### # store values needed for backward propagation in cache cache = (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) return a_next, c_next, yt_pred, cache
테스트 코드
np.random.seed(1) xt_tmp = np.random.randn(3,10) a_prev_tmp = np.random.randn(5,10) c_prev_tmp = np.random.randn(5,10) parameters_tmp = {} parameters_tmp['Wf'] = np.random.randn(5, 5+3) parameters_tmp['bf'] = np.random.randn(5,1) parameters_tmp['Wi'] = np.random.randn(5, 5+3) parameters_tmp['bi'] = np.random.randn(5,1) parameters_tmp['Wo'] = np.random.randn(5, 5+3) parameters_tmp['bo'] = np.random.randn(5,1) parameters_tmp['Wc'] = np.random.randn(5, 5+3) parameters_tmp['bc'] = np.random.randn(5,1) parameters_tmp['Wy'] = np.random.randn(2,5) parameters_tmp['by'] = np.random.randn(2,1) a_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp) print("a_next[4] = \n", a_next_tmp[4]) print("a_next.shape = ", a_next_tmp.shape) print("c_next[2] = \n", c_next_tmp[2]) print("c_next.shape = ", c_next_tmp.shape) print("yt[1] =", yt_tmp[1]) print("yt.shape = ", yt_tmp.shape) print("cache[1][3] =\n", cache_tmp[1][3]) print("len(cache) = ", len(cache_tmp))

2.2 Forward pass for LSTM
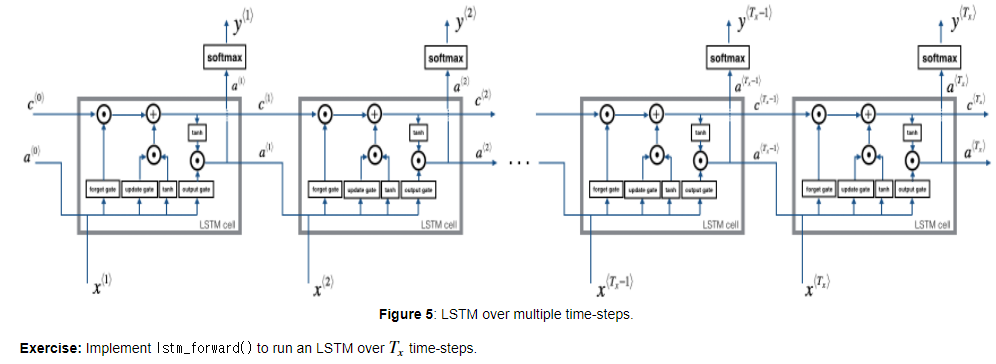
lstm_cell_forward 함수를 통해서 lstm_forward를 구현해봅니다.
def lstm_forward(x, a0, parameters): """ Implement the forward propagation of the recurrent neural network using an LSTM-cell described in Figure (4). Arguments: x -- Input data for every time-step, of shape (n_x, m, T_x). a0 -- Initial hidden state, of shape (n_a, m) parameters -- python dictionary containing: Wf -- Weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x) bf -- Bias of the forget gate, numpy array of shape (n_a, 1) Wi -- Weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x) bi -- Bias of the update gate, numpy array of shape (n_a, 1) Wc -- Weight matrix of the first "tanh", numpy array of shape (n_a, n_a + n_x) bc -- Bias of the first "tanh", numpy array of shape (n_a, 1) Wo -- Weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x) bo -- Bias of the output gate, numpy array of shape (n_a, 1) Wy -- Weight matrix relating the hidden-state to the output, numpy array of shape (n_y, n_a) by -- Bias relating the hidden-state to the output, numpy array of shape (n_y, 1) Returns: a -- Hidden states for every time-step, numpy array of shape (n_a, m, T_x) y -- Predictions for every time-step, numpy array of shape (n_y, m, T_x) c -- The value of the cell state, numpy array of shape (n_a, m, T_x) caches -- tuple of values needed for the backward pass, contains (list of all the caches, x) """ # Initialize "caches", which will track the list of all the caches caches = [] ### START CODE HERE ### Wy = parameters['Wy'] # saving parameters['Wy'] in a local variable in case students use Wy instead of parameters['Wy'] # Retrieve dimensions from shapes of x and parameters['Wy'] (≈2 lines) n_x, m, T_x = x.shape n_y, n_a = Wy.shape # initialize "a", "c" and "y" with zeros (≈3 lines) a = np.zeros((n_a, m, T_x)) c = np.zeros((n_a, m, T_x)) y = np.zeros((n_y, m, T_x)) # Initialize a_next and c_next (≈2 lines) a_next = a0 c_next = np.zeros((n_a, m)) # loop over all time-steps for t in range(T_x): # Get the 2D slice 'xt' from the 3D input 'x' at time step 't' xt = x[:,:,t] # Update next hidden state, next memory state, compute the prediction, get the cache (≈1 line) a_next, c_next, yt, cache = lstm_cell_forward(xt, a_next, c_next, parameters) # Save the value of the new "next" hidden state in a (≈1 line) a[:,:,t] = a_next # Save the value of the next cell state (≈1 line) c[:,:,t] = c_next # Save the value of the prediction in y (≈1 line) y[:,:,t] = yt # Append the cache into caches (≈1 line) caches.append(cache) ### END CODE HERE ### # store values needed for backward propagation in cache caches = (caches, x) return a, y, c, caches
매 time-step마다 lstm_cell_forward를 통해서 다음 time-step으로 전달되는 와 예측값 를 구해줍니다.
테스트코드
np.random.seed(1) x_tmp = np.random.randn(3,10,7) a0_tmp = np.random.randn(5,10) parameters_tmp = {} parameters_tmp['Wf'] = np.random.randn(5, 5+3) parameters_tmp['bf'] = np.random.randn(5,1) parameters_tmp['Wi'] = np.random.randn(5, 5+3) parameters_tmp['bi']= np.random.randn(5,1) parameters_tmp['Wo'] = np.random.randn(5, 5+3) parameters_tmp['bo'] = np.random.randn(5,1) parameters_tmp['Wc'] = np.random.randn(5, 5+3) parameters_tmp['bc'] = np.random.randn(5,1) parameters_tmp['Wy'] = np.random.randn(2,5) parameters_tmp['by'] = np.random.randn(2,1) a_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp) print("a[4][3][6] = ", a_tmp[4][3][6]) print("a.shape = ", a_tmp.shape) print("y[1][4][3] =", y_tmp[1][4][3]) print("y.shape = ", y_tmp.shape) print("caches[1][1][1] =\n", caches_tmp[1][1][1]) print("c[1][2][1]", c_tmp[1][2][1]) print("len(caches) = ", len(caches_tmp))

3. Backpropagation in RNN
RNN의 BP 과정을 살펴보고, 구현해보도록 하겠습니다.
3.1 Basic RNN backward pass
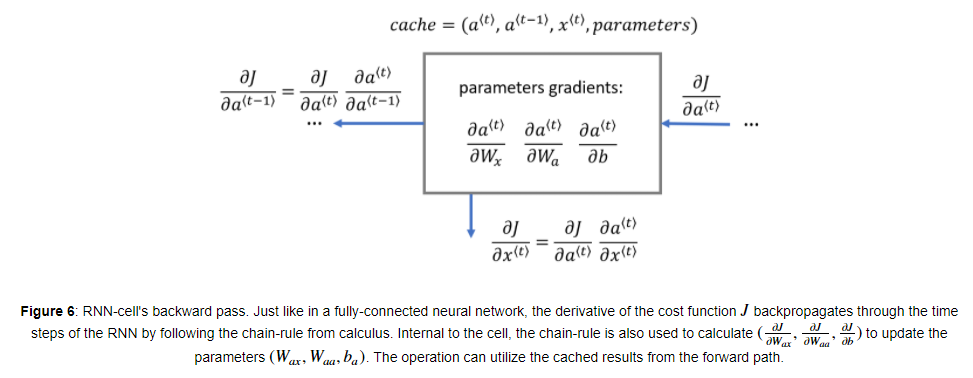
RNN cell의 backward 과정을 위와 같습니다. Fully-connected layer와 유사하게, Cost function에 대한 미분과 chain-rule을 따라서 Backpropagation throught the time step을 진행하면 됩니다.
cell의 내부에서 파라미터 를 업데이트하기 위해서 가 사용됩니다.
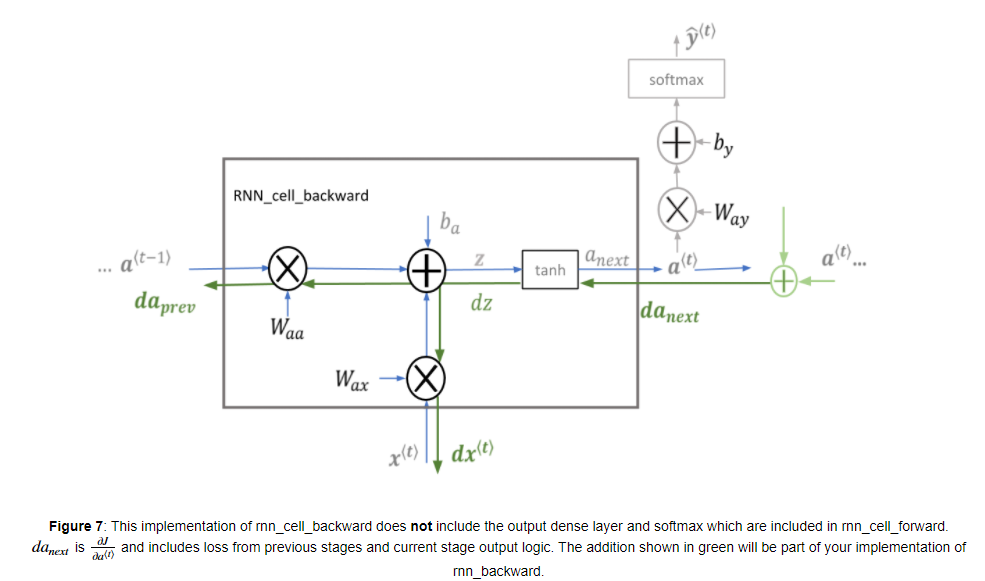
BP 공식은 다음과 같습니다.
cell에 전달되는 는 로 구할 수 있습니다.


def rnn_cell_backward(da_next, cache): """ Implements the backward pass for the RNN-cell (single time-step). Arguments: da_next -- Gradient of loss with respect to next hidden state cache -- python dictionary containing useful values (output of rnn_cell_forward()) Returns: gradients -- python dictionary containing: dx -- Gradients of input data, of shape (n_x, m) da_prev -- Gradients of previous hidden state, of shape (n_a, m) dWax -- Gradients of input-to-hidden weights, of shape (n_a, n_x) dWaa -- Gradients of hidden-to-hidden weights, of shape (n_a, n_a) dba -- Gradients of bias vector, of shape (n_a, 1) """ # Retrieve values from cache (a_next, a_prev, xt, parameters) = cache # Retrieve values from parameters Wax = parameters["Wax"] Waa = parameters["Waa"] Wya = parameters["Wya"] ba = parameters["ba"] by = parameters["by"] ### START CODE HERE ### # compute the gradient of the loss with respect to z (optional) (≈1 line) dz = (1 - a_next**2) * da_next # compute the gradient of the loss with respect to Wax (≈2 lines) dxt = Wax.T.dot(dz) dWax = dz.dot(xt.T) # compute the gradient with respect to Waa (≈2 lines) da_prev = Waa.T.dot(dz) dWaa = dz.dot(a_prev.T) # compute the gradient with respect to b (≈1 line) dba = np.sum(dz, keepdims=True, axis=-1) ### END CODE HERE ### # Store the gradients in a python dictionary gradients = {"dxt": dxt, "da_prev": da_prev, "dWax": dWax, "dWaa": dWaa, "dba": dba} return gradients
테스트코드
np.random.seed(1) xt_tmp = np.random.randn(3,10) a_prev_tmp = np.random.randn(5,10) parameters_tmp = {} parameters_tmp['Wax'] = np.random.randn(5,3) parameters_tmp['Waa'] = np.random.randn(5,5) parameters_tmp['Wya'] = np.random.randn(2,5) parameters_tmp['ba'] = np.random.randn(5,1) parameters_tmp['by'] = np.random.randn(2,1) a_next_tmp, yt_tmp, cache_tmp = rnn_cell_forward(xt_tmp, a_prev_tmp, parameters_tmp) da_next_tmp = np.random.randn(5,10) gradients_tmp = rnn_cell_backward(da_next_tmp, cache_tmp) print("gradients[\"dxt\"][1][2] =", gradients_tmp["dxt"][1][2]) print("gradients[\"dxt\"].shape =", gradients_tmp["dxt"].shape) print("gradients[\"da_prev\"][2][3] =", gradients_tmp["da_prev"][2][3]) print("gradients[\"da_prev\"].shape =", gradients_tmp["da_prev"].shape) print("gradients[\"dWax\"][3][1] =", gradients_tmp["dWax"][3][1]) print("gradients[\"dWax\"].shape =", gradients_tmp["dWax"].shape) print("gradients[\"dWaa\"][1][2] =", gradients_tmp["dWaa"][1][2]) print("gradients[\"dWaa\"].shape =", gradients_tmp["dWaa"].shape) print("gradients[\"dba\"][4] =", gradients_tmp["dba"][4])

전체 Backward pass thought the RNN은 다음과 같이 구현할 수 있습니다.
def rnn_backward(da, caches): """ Implement the backward pass for a RNN over an entire sequence of input data. Arguments: da -- Upstream gradients of all hidden states, of shape (n_a, m, T_x) caches -- tuple containing information from the forward pass (rnn_forward) Returns: gradients -- python dictionary containing: dx -- Gradient w.r.t. the input data, numpy-array of shape (n_x, m, T_x) da0 -- Gradient w.r.t the initial hidden state, numpy-array of shape (n_a, m) dWax -- Gradient w.r.t the input's weight matrix, numpy-array of shape (n_a, n_x) dWaa -- Gradient w.r.t the hidden state's weight matrix, numpy-arrayof shape (n_a, n_a) dba -- Gradient w.r.t the bias, of shape (n_a, 1) """ ### START CODE HERE ### # Retrieve values from the first cache (t=1) of caches (≈2 lines) (caches, x) = caches (a1, a0, x1, parameters) = caches[0] # Retrieve dimensions from da's and x1's shapes (≈2 lines) n_a, m, T_x = da.shape n_x, m = x1.shape # initialize the gradients with the right sizes (≈6 lines) dx = np.zeros((n_x, m, T_x)) dWax = np.zeros((n_a, n_x)) dWaa = np.zeros((n_a, n_a)) dba = np.zeros((n_a, 1)) da0 = np.zeros((n_a, m)) da_prevt = np.zeros((n_a, m)) # Loop through all the time steps for t in reversed(range(T_x)): # Compute gradients at time step t. # Remember to sum gradients from the output path (da) and the previous timesteps (da_prevt) (≈1 line) gradients = rnn_cell_backward(da[:,:,t] + da_prevt, caches[t]) # Retrieve derivatives from gradients (≈ 1 line) dxt, da_prevt, dWaxt, dWaat, dbat = gradients["dxt"], gradients["da_prev"], gradients["dWax"], gradients["dWaa"], gradients["dba"] # Increment global derivatives w.r.t parameters by adding their derivative at time-step t (≈4 lines) dx[:, :, t] = dxt dWax += dWaxt dWaa += dWaat dba += dbat # Set da0 to the gradient of a which has been backpropagated through all time-steps (≈1 line) da0 = da_prevt ### END CODE HERE ### # Store the gradients in a python dictionary gradients = {"dx": dx, "da0": da0, "dWax": dWax, "dWaa": dWaa,"dba": dba} return gradients
reversed(range(T_x))를 통해서 forward의 역방향으로 진행하며, 매 BPTT마다 rnn_cell_backward 함수를 통해서 backward를 수행합니다.
테스트코드
np.random.seed(1) x_tmp = np.random.randn(3,10,4) a0_tmp = np.random.randn(5,10) parameters_tmp = {} parameters_tmp['Wax'] = np.random.randn(5,3) parameters_tmp['Waa'] = np.random.randn(5,5) parameters_tmp['Wya'] = np.random.randn(2,5) parameters_tmp['ba'] = np.random.randn(5,1) parameters_tmp['by'] = np.random.randn(2,1) a_tmp, y_tmp, caches_tmp = rnn_forward(x_tmp, a0_tmp, parameters_tmp) da_tmp = np.random.randn(5, 10, 4) gradients_tmp = rnn_backward(da_tmp, caches_tmp) print("gradients[\"dx\"][1][2] =", gradients_tmp["dx"][1][2]) print("gradients[\"dx\"].shape =", gradients_tmp["dx"].shape) print("gradients[\"da0\"][2][3] =", gradients_tmp["da0"][2][3]) print("gradients[\"da0\"].shape =", gradients_tmp["da0"].shape) print("gradients[\"dWax\"][3][1] =", gradients_tmp["dWax"][3][1]) print("gradients[\"dWax\"].shape =", gradients_tmp["dWax"].shape) print("gradients[\"dWaa\"][1][2] =", gradients_tmp["dWaa"][1][2]) print("gradients[\"dWaa\"].shape =", gradients_tmp["dWaa"].shape) print("gradients[\"dba\"][4] =", gradients_tmp["dba"][4]) print("gradients[\"dba\"].shape =", gradients_tmp["dba"].shape)

3.2 LSTM backward pass
3.2.1 One Step backward
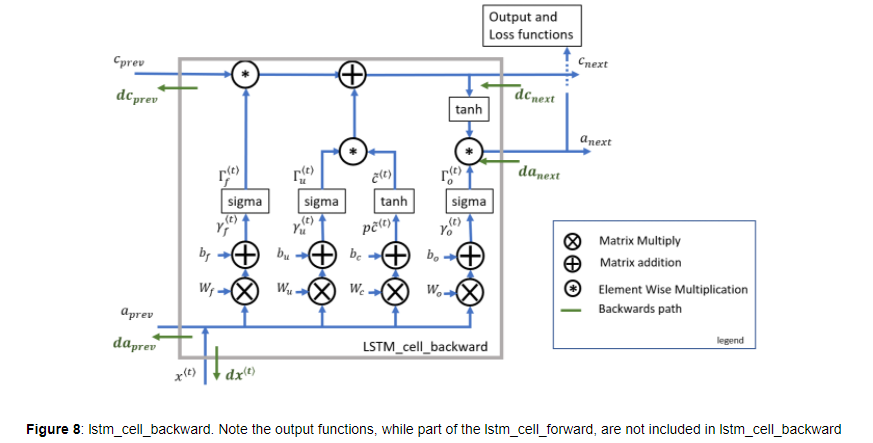
LSTM의 backward는 조금 복잡한데, 흐름은 위와 같습니다.
3.2.2 gate derivatives
각 gate에서의 미분공식은 다음과 같습니다.
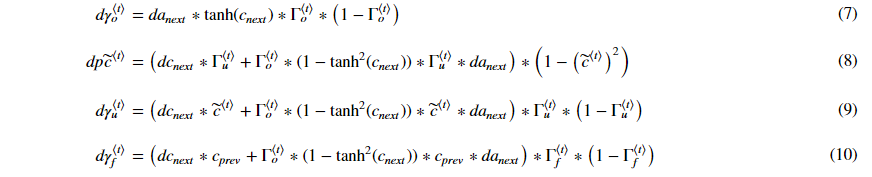
3.2.3 parameter derivatives
각 parameter의 미분공식입니다.
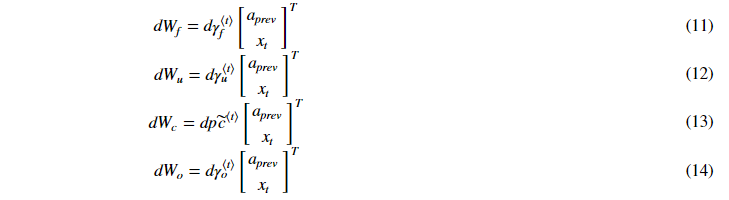

마지막으로 는 아래와 같이 계산할 수 있습니다.

아래는 LSTM cell에서의 backward 코드입니다.
def lstm_cell_backward(da_next, dc_next, cache): """ Implement the backward pass for the LSTM-cell (single time-step). Arguments: da_next -- Gradients of next hidden state, of shape (n_a, m) dc_next -- Gradients of next cell state, of shape (n_a, m) cache -- cache storing information from the forward pass Returns: gradients -- python dictionary containing: dxt -- Gradient of input data at time-step t, of shape (n_x, m) da_prev -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m) dc_prev -- Gradient w.r.t. the previous memory state, of shape (n_a, m, T_x) dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x) dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x) dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x) dWo -- Gradient w.r.t. the weight matrix of the output gate, numpy array of shape (n_a, n_a + n_x) dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1) dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1) dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1) dbo -- Gradient w.r.t. biases of the output gate, of shape (n_a, 1) """ # Retrieve information from "cache" (a_next, c_next, a_prev, c_prev, ft, it, cct, ot, xt, parameters) = cache ### START CODE HERE ### # Retrieve dimensions from xt's and a_next's shape (≈2 lines) n_x, m = xt.shape n_a, m = a_next.shape # Compute gates related derivatives, you can find their values can be found by looking carefully at equations (7) to (10) (≈4 lines) dot = da_next * np.tanh(c_next) * ot * (1-ot) dcct = (dc_next * it + ot * (1-np.square(np.tanh(c_next))) * it * da_next) * (1-np.square(cct)) dit = (dc_next * cct + ot*(1-np.square(np.tanh(c_next)))*cct*da_next) * it * (1-it) dft = (dc_next * c_prev + ot*(1-np.square(np.tanh(c_next))) * c_prev * da_next) * ft * (1-ft) # Compute parameters related derivatives. Use equations (11)-(18) (≈8 lines) dWf = np.dot(dft,np.concatenate((a_prev, xt), axis=0).T) dWi = np.dot(dit,np.concatenate((a_prev, xt), axis=0).T) dWc = np.dot(dcct,np.concatenate((a_prev, xt), axis=0).T) dWo = np.dot(dot,np.concatenate((a_prev, xt), axis=0).T) dbf = np.sum(dft,axis=1,keepdims=True) dbi = np.sum(dit,axis=1,keepdims=True) dbc = np.sum(dcct,axis=1,keepdims=True) dbo = np.sum(dot,axis=1,keepdims=True) # Compute derivatives w.r.t previous hidden state, previous memory state and input. Use equations (19)-(21). (≈3 lines) da_prev = np.dot(parameters['Wf'][:,:n_a].T,dft)+np.dot(parameters['Wi'][:,:n_a].T,dit)+np.dot(parameters['Wc'][:,:n_a].T,dcct)+np.dot(parameters['Wo'][:,:n_a].T,dot) dc_prev = dc_next*ft+ot*(1-np.square(np.tanh(c_next)))*ft*da_next dxt = np.dot(parameters['Wf'][:,n_a:].T,dft)+np.dot(parameters['Wi'][:,n_a:].T,dit)+np.dot(parameters['Wc'][:,n_a:].T,dcct)+np.dot(parameters['Wo'][:,n_a:].T,dot) ### END CODE HERE ### # Save gradients in dictionary gradients = {"dxt": dxt, "da_prev": da_prev, "dc_prev": dc_prev, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi, "dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo} return gradients
테스트코드
np.random.seed(1) xt_tmp = np.random.randn(3,10) a_prev_tmp = np.random.randn(5,10) c_prev_tmp = np.random.randn(5,10) parameters_tmp = {} parameters_tmp['Wf'] = np.random.randn(5, 5+3) parameters_tmp['bf'] = np.random.randn(5,1) parameters_tmp['Wi'] = np.random.randn(5, 5+3) parameters_tmp['bi'] = np.random.randn(5,1) parameters_tmp['Wo'] = np.random.randn(5, 5+3) parameters_tmp['bo'] = np.random.randn(5,1) parameters_tmp['Wc'] = np.random.randn(5, 5+3) parameters_tmp['bc'] = np.random.randn(5,1) parameters_tmp['Wy'] = np.random.randn(2,5) parameters_tmp['by'] = np.random.randn(2,1) a_next_tmp, c_next_tmp, yt_tmp, cache_tmp = lstm_cell_forward(xt_tmp, a_prev_tmp, c_prev_tmp, parameters_tmp) da_next_tmp = np.random.randn(5,10) dc_next_tmp = np.random.randn(5,10) gradients_tmp = lstm_cell_backward(da_next_tmp, dc_next_tmp, cache_tmp) print("gradients[\"dxt\"][1][2] =", gradients_tmp["dxt"][1][2]) print("gradients[\"dxt\"].shape =", gradients_tmp["dxt"].shape) print("gradients[\"da_prev\"][2][3] =", gradients_tmp["da_prev"][2][3]) print("gradients[\"da_prev\"].shape =", gradients_tmp["da_prev"].shape) print("gradients[\"dc_prev\"][2][3] =", gradients_tmp["dc_prev"][2][3]) print("gradients[\"dc_prev\"].shape =", gradients_tmp["dc_prev"].shape) print("gradients[\"dWf\"][3][1] =", gradients_tmp["dWf"][3][1]) print("gradients[\"dWf\"].shape =", gradients_tmp["dWf"].shape) print("gradients[\"dWi\"][1][2] =", gradients_tmp["dWi"][1][2]) print("gradients[\"dWi\"].shape =", gradients_tmp["dWi"].shape) print("gradients[\"dWc\"][3][1] =", gradients_tmp["dWc"][3][1]) print("gradients[\"dWc\"].shape =", gradients_tmp["dWc"].shape) print("gradients[\"dWo\"][1][2] =", gradients_tmp["dWo"][1][2]) print("gradients[\"dWo\"].shape =", gradients_tmp["dWo"].shape) print("gradients[\"dbf\"][4] =", gradients_tmp["dbf"][4]) print("gradients[\"dbf\"].shape =", gradients_tmp["dbf"].shape) print("gradients[\"dbi\"][4] =", gradients_tmp["dbi"][4]) print("gradients[\"dbi\"].shape =", gradients_tmp["dbi"].shape) print("gradients[\"dbc\"][4] =", gradients_tmp["dbc"][4]) print("gradients[\"dbc\"].shape =", gradients_tmp["dbc"].shape) print("gradients[\"dbo\"][4] =", gradients_tmp["dbo"][4]) print("gradients[\"dbo\"].shape =", gradients_tmp["dbo"].shape)
3.3 Backward pass through the LSTM RNN
전체 Backward 과정은 rnn_backward 함수와 유사합니다. 마찬가지로 마지막 time-step부터 역으로 진행하면서 각 cell에서 미분값을 구하고, 파라미터를 업데이트하게 됩니다.
def lstm_backward(da, caches): """ Implement the backward pass for the RNN with LSTM-cell (over a whole sequence). Arguments: da -- Gradients w.r.t the hidden states, numpy-array of shape (n_a, m, T_x) caches -- cache storing information from the forward pass (lstm_forward) Returns: gradients -- python dictionary containing: dx -- Gradient of inputs, of shape (n_x, m, T_x) da0 -- Gradient w.r.t. the previous hidden state, numpy array of shape (n_a, m) dWf -- Gradient w.r.t. the weight matrix of the forget gate, numpy array of shape (n_a, n_a + n_x) dWi -- Gradient w.r.t. the weight matrix of the update gate, numpy array of shape (n_a, n_a + n_x) dWc -- Gradient w.r.t. the weight matrix of the memory gate, numpy array of shape (n_a, n_a + n_x) dWo -- Gradient w.r.t. the weight matrix of the save gate, numpy array of shape (n_a, n_a + n_x) dbf -- Gradient w.r.t. biases of the forget gate, of shape (n_a, 1) dbi -- Gradient w.r.t. biases of the update gate, of shape (n_a, 1) dbc -- Gradient w.r.t. biases of the memory gate, of shape (n_a, 1) dbo -- Gradient w.r.t. biases of the save gate, of shape (n_a, 1) """ # Retrieve values from the first cache (t=1) of caches. (caches, x) = caches (a1, c1, a0, c0, f1, i1, cc1, o1, x1, parameters) = caches[0] ### START CODE HERE ### # Retrieve dimensions from da's and x1's shapes (≈2 lines) n_a, m, T_x = da.shape n_x, m = x1.shape # initialize the gradients with the right sizes (≈12 lines) dx = np.zeros((n_x, m, T_x)) da0 = np.zeros((n_a, m)) da_prevt = np.zeros((n_a, m)) dc_prevt = np.zeros((n_a, m)) dWf = np.zeros((n_a, n_a + n_x)) dWi = np.zeros((n_a, n_a + n_x)) dWc = np.zeros((n_a, n_a + n_x)) dWo = np.zeros((n_a, n_a + n_x)) dbf = np.zeros((n_a, 1)) dbi = np.zeros((n_a, 1)) dbc = np.zeros((n_a, 1)) dbo = np.zeros((n_a, 1)) # loop back over the whole sequence for t in reversed(range(T_x)): # Compute all gradients using lstm_cell_backward gradients = lstm_cell_backward(da[:,:,t]+da_prevt, dc_prevt, caches[t]) # Store or add the gradient to the parameters' previous step's gradient da_prevt = gradients["da_prev"] dc_prevt = gradients["dc_prev"] dx[:,:,t] = gradients["dxt"] dWf = dWf+gradients["dWf"] dWi = dWi+gradients["dWi"] dWc = dWc+gradients["dWc"] dWo = dWo+gradients["dWo"] dbf = dbf+gradients["dbf"] dbi = dbi+gradients["dbi"] dbc = dbc+gradients["dbc"] dbo = dbo+gradients["dbo"] # Set the first activation's gradient to the backpropagated gradient da_prev. da0 = gradients["da_prev"] ### END CODE HERE ### # Store the gradients in a python dictionary gradients = {"dx": dx, "da0": da0, "dWf": dWf,"dbf": dbf, "dWi": dWi,"dbi": dbi, "dWc": dWc,"dbc": dbc, "dWo": dWo,"dbo": dbo} return gradients
테스트코드
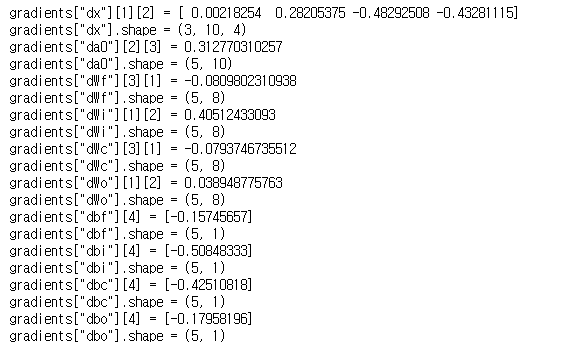
np.random.seed(1) x_tmp = np.random.randn(3,10,7) a0_tmp = np.random.randn(5,10) parameters_tmp = {} parameters_tmp['Wf'] = np.random.randn(5, 5+3) parameters_tmp['bf'] = np.random.randn(5,1) parameters_tmp['Wi'] = np.random.randn(5, 5+3) parameters_tmp['bi'] = np.random.randn(5,1) parameters_tmp['Wo'] = np.random.randn(5, 5+3) parameters_tmp['bo'] = np.random.randn(5,1) parameters_tmp['Wc'] = np.random.randn(5, 5+3) parameters_tmp['bc'] = np.random.randn(5,1) parameters_tmp['Wy'] = np.zeros((2,5)) # unused, but needed for lstm_forward parameters_tmp['by'] = np.zeros((2,1)) # unused, but needed for lstm_forward a_tmp, y_tmp, c_tmp, caches_tmp = lstm_forward(x_tmp, a0_tmp, parameters_tmp) da_tmp = np.random.randn(5, 10, 4) gradients_tmp = lstm_backward(da_tmp, caches_tmp) print("gradients[\"dx\"][1][2] =", gradients_tmp["dx"][1][2]) print("gradients[\"dx\"].shape =", gradients_tmp["dx"].shape) print("gradients[\"da0\"][2][3] =", gradients_tmp["da0"][2][3]) print("gradients[\"da0\"].shape =", gradients_tmp["da0"].shape) print("gradients[\"dWf\"][3][1] =", gradients_tmp["dWf"][3][1]) print("gradients[\"dWf\"].shape =", gradients_tmp["dWf"].shape) print("gradients[\"dWi\"][1][2] =", gradients_tmp["dWi"][1][2]) print("gradients[\"dWi\"].shape =", gradients_tmp["dWi"].shape) print("gradients[\"dWc\"][3][1] =", gradients_tmp["dWc"][3][1]) print("gradients[\"dWc\"].shape =", gradients_tmp["dWc"].shape) print("gradients[\"dWo\"][1][2] =", gradients_tmp["dWo"][1][2]) print("gradients[\"dWo\"].shape =", gradients_tmp["dWo"].shape) print("gradients[\"dbf\"][4] =", gradients_tmp["dbf"][4]) print("gradients[\"dbf\"].shape =", gradients_tmp["dbf"].shape) print("gradients[\"dbi\"][4] =", gradients_tmp["dbi"][4]) print("gradients[\"dbi\"].shape =", gradients_tmp["dbi"].shape) print("gradients[\"dbc\"][4] =", gradients_tmp["dbc"][4]) print("gradients[\"dbc\"].shape =", gradients_tmp["dbc"].shape) print("gradients[\"dbo\"][4] =", gradients_tmp["dbo"][4]) print("gradients[\"dbo\"].shape =", gradients_tmp["dbo"].shape)
'Coursera 강의 > Deep Learning' 카테고리의 다른 글
| Introduction to Word Embeddings (0) | 2020.12.24 |
|---|---|
| [실습] Character-level Language Modeling (0) | 2020.12.21 |
| Recurrent Neural Networks 2 (GRU, LSTM, BRNN) (0) | 2020.12.21 |
| Recurrent Neural Networks 1 (Basic of RNN model) (0) | 2020.12.20 |
| Neural Style Transfer (0) | 2020.12.01 |




댓글