해당 내용은 Coursera의 딥러닝 특화과정(Deep Learning Specialization)의 다섯 번째 강의 Sequence Models를 듣고 정리한 내용입니다. (Week 1)
[Why sequence models]
다섯번째 강의에서는 Sequence model에 대해서 배운다. 딥러닝에서 가장 흥미로운 분야 중 하나이며, Recurrent Neural Network(RNN)같은 모델은 음성 인식, 자연어 처리(NLP) 영역에 영향을 끼쳤다.
아래는 시퀀스 모델이 사용되는 몇 가지 예시들이다.

음성 인식(Speech recognition)의 경우에는 Input X인 오디오가 Text output Y에 매핑된다. 입력과 출력 모두 시퀀스 데이터인데, X는 시간에 따라 재생되는 음성이며, Y는 단어 시퀀스이다.
음악 생성(Music generation)의 경우에는 Output Y만 시퀀스 데이터이고, 입력은 빈 집합이거나 단일 정수, 또는 생성하려는 음악의 장르나 원하는 음악의 처음 몇 개의 음일 수 있다.
감정 분류(Sentiment classification)에서 Input X는 시퀀스 데이터이고, 주어진 문장에 대해서 Output은 별점이 될 수 있다.
시퀀스 모델은 DNA Sequence 분석에도 매우 유용한데, DNA 염기 서열을 살펴보고 어떤 부분이 일치하는지 라벨을 붙이는 것과 같은 일들을 할 수 있다.
그 밖에도 기계번역(Machine Translation), 비디오 동작 인식, 이름 인식 등이 있다.
[Notation]
다음으로 RNN에서 사용되는 용어들을 정리한다.

예를 들어서 'Harry Potter and Herimone Granger invented a new spell'이라는 input 가 있고, 이 문장에서 이름을 인식(Name entity recognition)한다고 했을 때, 각 단어마다 output y를 가지며, output값은 이름인지 아닌지에 대한 1/0의 값을 가진다.
이번 예시에서는 입력 시퀀스 x가 총 9개의 단어로 이루어져 있고, 입력은 총 9개의 feature set을 가지게 된다. 시퀀스의 순서를 나타내기 위해서 위첨자로 \(x^{<1>}, x^{<2>}, \cdots, x^{<t>}, \cdots, x^{<9>}\)로 나타내어서 순서를 나타낸다. 여기서 위첨자 t를 통해서 순서를 나타내며, t는 time sequence에서 유래한다.
유사하게 output y에 대해서도 \(y^{<1>}, y^{<2>}, \cdots, y^{<9>}\)로 나타낸다.
시퀀스의 길이는 T에 아래첨자 x를 사용해서 \(T_x\)로 나타내며 여기서는 \(T_x = 9\)이다.
\(T_y\)는 출력 시퀀스의 길이를 의미하며, 여기서는 \(T_x\)와 동일한 값을 가지지만, 다른 값을 가질 수도 있다.
그리고 여러개의 training data가 있을 때, 이전과 동일하게 (i)를 위첨자에 사용해서 i번째 training data를 나타내서, \(x^{(i)<t>}\)로 나타내며, \(T_x\)가 한 시퀀스의 길이를 뜻하므로, training set의 서로 다른 데이터의 길이는 다를 수 있고, i번째 트레이닝 데이터의 길이는 \(T_x^{(i)}\)로 표기한다.
다음으로 NLP, 자연어 처리를 다루는 방법에 대해서 이야기해보자.
NLP에서 먼저 결정해야할 것은 시퀀스의 단어 표현 방법이다. 'Harry'라는 단어를 어떻게 표현해야할까?
시퀀스의 단어를 표현하기 위해서는 먼저 Vocabulary(or Dictionary)를 만들어야 한다.
예를 들어 Voca의 첫번째 단어는 'a'이고, 두번째는 'Aaron', 조금 더 지나가면 'and', 또 더 살펴보다보면 'Harry', 'Potter'가 나오고 마지막에는 'Zulu'가 나올 수 있다.
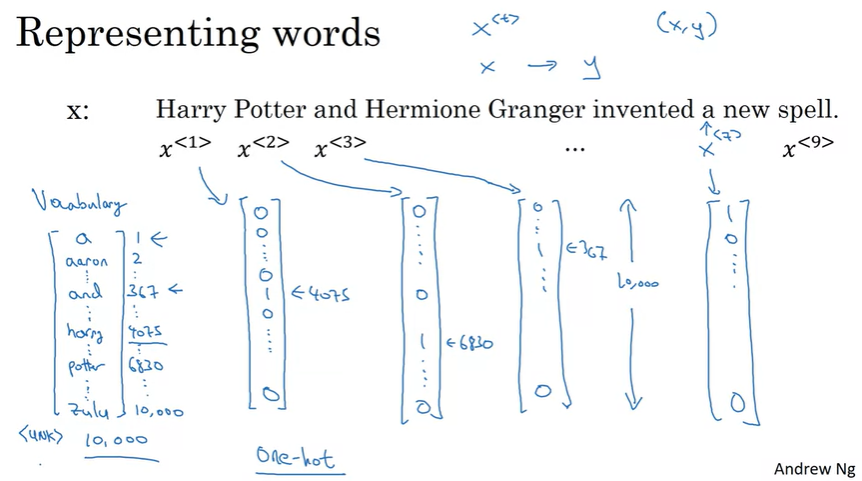
여기서 'harry'는 4075번째, 'potter'는 6830번째에 나왔다. 보통 상용 어플리케이션용의 사전은 대게 3~5만개의 단어를 포함한다. 여기서는 1만개를 사용한다고 가정한다.(단어를 고르는 방법은 자주 사용하는 단어 1만개를 고르거나, 다른 방법을 사용할 수도 있다)
그 다음에 단어를 one hot encoding을 통해서 표현한다.
예를 들어, 'harry'를 나타내는 단어 \(x^{<1>}\)는 4075번째 위치만 1이고 나머지는 0인 벡터이다.(사전의 4075번째 위치가 'harry'이기 때문)
\(x^{<2>}\) 역시 6830번째만 1이고 나머지는 0인 벡터이다.
(one hot은 하나만 1이고 나머지는 0이라는 의미에서 유래)
단어를 표현했으면, 다음 목표는 이렇게 표현된 input x를 output y로 매핑하는 시퀀스 모델을 학습하는 것이다.
Supervised Learning으로 수행되고, x와 y를 포함하는 데이터를 사용한다.
만약에 Voca에 없는 단어가 나오면 어떻게 할까?
그 답은 새로운 Token이나 모르는 단어를 의미하는 가짜 단어를 만들면된다. 즉, <UNK>와 같이 표시해서 Voca에 없는 단어를 나타낼 수 있다.

[Recurrent Neural Network Model]
RNN 모델에 대해서 살펴보기 전에 기본적인 모델에 대해서 이야기해보자.
이전 예제처럼 9개의 입력 단어가 있을 때, 9개의 단어를 입력으로 받는 모델을 그려보도록 하자. 그렇다면 9개의 one-hot 벡터가 모델에 입력된다. 그리고 몇 개의 hidden layer를 통해서 최종적으로 0 혹은 1의 값을 갖는 9개의 output이 나오게 될 것이다.(1은 사람 이름을 뜻함)

하지만 위와 같은 방법은 잘 동작하지 않는다.
2가지 문제점이 존재하는데,
첫번째는 입력과 출력 데이터의 길이가 트레이닝 데이터마다 다르다. 모든 트레이닝 데이터가 같은 입력 길이 \(T_x\)를 가지지 않고, 같은 \(T_y\)를 가지지 않는다. 입력에 임의의 값이나 0으로 채워서 최대 길이로 동일하게 맞출 수는 있지만 좋은 방법은 아니다.
두번째는 이런 naive 신경망에서는 텍스트의 서로 다른 위치에 있는 동일한 feature(단어)가 공유되지 않는다. 즉, 이름이 첫번째 위치나 t번째 위치에서 나오거나 동일하게 사람 이름이라고 추론하는 것이 올바르다. 이는 CNN에서 학습한 이미지의 특성을 이미지의 다른 부분에 일반화시키는 것과 유사하다.
또한, 이 경우에 각각의 단어가 1만 차원의 one-hot vector이기 때문에 입력 데이터가 매우 크고, 파라미터의 수가 엄청나게 많아 진다.
그렇다면 Recurrent Neural Network(순환신경망)은 무엇일까?

RNN의 기본 구조는 위와 같다. 좌에서 우로 문장을 읽는다면 처음 읽는 단어 \(x^{<1>}\)를 신경망의 입력으로 사용한다. 그리고 내부 신경망(hidden layer, output layer)를 통해서 사람 이름의 일부인지 예측한다.
그리고 문장의 두번째 단어 \(x^{<2>}\)를 읽고, \(y^{<2>}\)를 예측할 때, \(x^{<2>}\)만 사용하는 것이 아니라, 첫번째 단어로 연산한 정보의 일부를 사용하게 된다. 구체적으로는 첫번째 시점의 activation이 두번째 시점에 전달된다.
이런 식으로 진행해서 마지막 시점에서 \(x^{<T_x>}\)로 \(y^{<T_y>}\)를 예측한다.
(해당 예제에서는 \(T_x = T_y\)이다.)
그리고 RNN 신경망 학습을 시작하기 전에 \(a^{<0>}\)이 사용되는 것을 볼 수 있는데, 이것은 보통 무작위로 초기화하거나, 0으로 초기화한다. 0으로 초기화하는 경우가 가장 일반적이다.

위 이미지 오른쪽처럼 하나의 NN만 표현하고 순환하는 표시로 RNN을 표현하기도 한다. 이는 매 시점에서 파라미터를 공유한다는 것을 의미한다. (\(W_{aa}, W_{ax}, W_{ya}\)가 사용됨)
위 기본 RNN 모델의 단점은, 앞서 나온 정보만을 사용해서 예측을 한다는 것이다. \(y^{<3>}\)을 예측할 때, \(x^{<4>}, x^{<5>}, x^{<6>}\)의 정보를 사용하지 않는다. 이는 문제가 될 수 있다.

위와 같은 문장이 주어졌을 때, 첫 두 단어의 정보뿐만 아니라 뒤에 있는 나머지 단어들의 정보를 아는 것도 매우 유용할 것이다. 즉, 첫 두세마디만 고려한다면, Teddy라는 단어가 사람의 이름인지 확실하게 알 수 없다는 것이다.
아래 문장도 마찬가지이다. 첫 두세마디 만으로는 차이를 구별할 수 없다. 이 문제는 양방향으로 반복되는 BRNN을 통해서 해결될 수 있다.
RNN의 Forward Propagation
아래는 신경망이 어떻게 계산되는지 보여주고 있다.

초기에 사용되는 \(a^{<0>}\)는 일반적으로 0 vector로 초기화된다.
다음으로 \(a^{<1>}\)을 구하기 위해서 \(W_{aa}a^{<0>} + W_{ax}x^{<1>} + b_a\)에 activation function을 적용한다.
\[a^{<1>} = g_1(W_{aa}a^{<0>} + W_{ax}x^{<1>} + b_a)\]
activation function으로는 tanh나 ReLU가 사용된다.
그리고 첫번째 단어의 예측 \(\hat{y}^{<1>}\)은 다음과 같이 구할 수 있다.
\[\hat{y}^{<1>} = g_2(W_{ya}a^{<1>} + b_y)\]
따라서 일반화하면 다음과 같다.
\[\begin{align*} a^{<t>} &= g(W_{aa}a^{<t-1>} + W_{ax}x^{<t>} + b_a) \\ \hat{y}^{<t>} &= g(W_{ya}a^{<t>} + b_y) \end{align*}\]
그리고, 위 식을 조금 단순화시키면 다음과 같이 표현할 수 있다.

\[a^{<t>} = g(W_a [a^{<t-1>}, x^{<t>}] + b_a)\]
\(W_a\)는 \([W_{aa} \vdots W_{ax}]\)를 의미하는데, 만약 a가 100차원이고, x가 10,000차원의 벡터라면 \(W_{aa}\)는 (100, 100)의 차원을 갖고, \(W_{ax}\)는 (100, 10000)의 차원을 갖게 되고, 두 가중치를 연결하면 \(W_a\)는 (100, 10100) 차원의 가중치가 되는 것이다.
\(W_a\)와 연산되는 \([a^{<t-1>}, x^{<t>}]\)는 \(\begin{bmatrix} a^{<t-1>} \\ x^{t} \end{bmatrix}\)를 의미하고, 10100 차원의 벡터가 된다.
\[\hat{y}^{<t>} = g(W_{y}a^{<t>} + b_y)\]
\(\hat{y}^{<t>}\)는 위와 같이 간단하게 표현할 수 있다.
[Backpropagation through time]
다음으로 RNN의 Backpropagation(역전파)가 어떻게 동작하는지 대략적으로 살펴보자.

이미 알겠지만, BP는 FP의 반대반향으로 진행된다.

일단 이전 강의 내용에서 살펴봤듯이, \(W_a, b_a\)를 통해서 \(a^{<t>}\)를 구하고, \(W_y, b_y\)를 통해서 예측값 \(\hat{y}^{<t>}\)를 구한다.
그리고 BP를 계산하고 위해 Loss function을 통해서 실제 결과와 예측값의 Loss(cost)를 계산하고, 총 Loss의 값을 구한다.
Cross Entropy Loss(Logistic Regression Loss)를 사용할 수 있는데, 각 element의 Loss와 총 Loss는 다음과 같다.
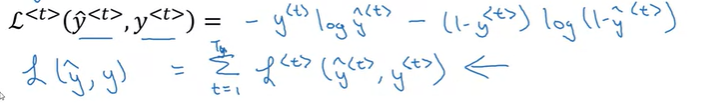
최종 Loss는 시간별 개별 Loss의 합이다.
그리고 BP를 진행하는데, BP는 오른쪽에서 왼쪽으로 향하는 계산이다.

FP가 시간 순서로 전달하는 것과 반대로 BP는 시간을 거꾸로 가는 것과 같아서 Backpropagation through time(BPTT)라고 부른다.

[Difference types of RNNs]
지금까지 RNN 아키텍처에서는 \(T_x\)가 \(T_y\)와 동일한 경우를 살펴보았다. \(T_x, T_y\)는 항상 같지 않을 수 있으며, 다양한 RNN 아키텍처를 살펴보도록 하자.

강의 초기에 보여준 시퀀스 데이터의 예시들이다. x, y가 모두 시퀀스 데이터거나, x가 빈 집합일 수도 있거나, 하나의 입력일 수 있으며, y가 시퀀스가 아닐 수도 있다.
이전 예제들처럼, \(T_x = T_y\)라면 Many-to-many 아키텍처라고 하고, 아래와 같이 모델링할 수 있다.

만약 Sentiment classification처럼 x는 텍스트이지만, y가 0/1의 값을 갖는 output이라면 Many-to-one 아키텍처로 다음과 같이 모델링 할 수 있다.

물론 one-to-one 아키텍처도 있으며, 단순한 신경망과 동일하다.

Music generation과 같은 모델은 입력이 정수일 수도 있고, 어떤 음악 장르나 원하는 음악의 첫 음표일 수도 있으며, 어느 것도 입력하고 싶지 않다면 null 입력일 수도 있고, 항상 0일 수도 있다. 이런 모델은 One-to-many 아키텍처이며, 다음과 같이 하나의 input x와 시퀀스 output y를 가질 수 있는 모델이 된다.

아키텍처는 이렇게 Many-to-many, Many-to-one, One-to-one, One-to-many으로 분류할 수 있는데, Many-to-many에서 다른 아키텍처들도 있다.
기계번역(machine translation)는 Many-to-many 아키텍처지만, 입력과 출력의 길이가 다를 수 있다.(\(T_x != T_y\))

위와 같은 모델에서 입력을 받는 부분은 encoder, 그리고 출력을 내는 부분을 decoder라고 부른다.

[Language model and sequence generation]
Language Modelling은 LNP에서 가장 기본적이고 중요한 작업 중 하나이다. 이번 강의에서 RNN을 사용해서 Language model을 만드는 방법을 배워보도록 할것이다.
language modelling(언어 모델)이란 무엇일까?
우리가 음성 인식(Speech recognition) 시스템을 만들고 있다고 가정해보자.

The apple and pear salad라는 문장을 들었을 때, 위 두 가지 문장이 있다면 두 번째 문장이 더 가능성이 있다고 생각할 것이다. 여기서 두 번째 문장을 선택하는 방법은 두 문장의 확률이 얼마인지 알려주는 언어 모델을 사용하는 것이다.
예를 들어서, 모델이 첫 번째 문장에 대한 확률은 \(3.2 \times 10^{-13}\)으로 지정하고, 두 번째 문장의 확률은 \(5.7 \times 10^{-10}\)으로 지정하는 것이다. 따라서 음성 인식 시스템은 두번째 문장을 선택하게 된다.

이러한 언어 모델은 RNN을 사용해서 만들 수 있는데, 이런 모델을 만드려면 large corpus of english text를 포함하는 training set이 필요하다. (corpus라는 단어는 NLP 용어로 큰 영어 문장들을 의미한다.)
언어 모델의 기본 작업은 문장을 입력하는 것인데, 이 문장은 \(y^{<1>}, y^{<2>}, \cdots\)로 표현하겠다. 언어 모델에서 문장을 input x가 아닌 output y로 표시하는 것이 유용하다.

위와 같은 'Cats average 15 hours of sleep a day.'라는 문장이 있다고 해보자.
첫 번째로 해야할 일은 이 문장을 토큰화하는 것이다. 토큰화를 통해서 단어들로 분리하고, 단어들을 Voca의 index를 통해 one-hot vector로 매핑한다. 한 가지 추가 작업으로는 문장이 끝난다는 의미인 <EOS>라는 토큰을 추가한다.4
(마침표를 토큰으로 사용할 수 있는데, 여기서 마침표는 무시했다.)
만약 아래 문장처럼 Mau라는 단어가 Voca에 없다면 <UNK>라는 토큰으로 대체할 수 있다.
그리고 RNN 아키텍처는 다음과 같다.

첫 번째 \(x^{<1>}\)와 \(a^{<0>}\)은 0 vector로 설정하고, \(a^{<1>}\)과 \(\hat{y}^{<1>}\)를 계산한다.
여기서 \(\hat{y}^{<1>}\)는 softmax output이며, 첫 번째 단어가 존재할 확률을 의미한다. 이 예제에서는 첫 번째 단어 cats가 될 것이다.
그리고 다음 RNN step이 진행되고 \(a^{<1>}\)를 가지고 다음 단계를 진행한다. 여기서 \(x^{<2>}\)는 \(y^{<1>}\)가 되며, 우리는 이제 모델에 올바른 첫 단어인 cats를 입력하게 된다.
그리고 이 단계에서 softmax output에 의해서 다시 예측되고 그 결과는 첫 번째 단어가 cats일 때의 다른 Voca 단어들의 확률이 될 것이다.
그리고 세번째 단계에서 \(x^{<3>} = y^{<2>}\)이고, 이전 단어 'cats average'를 가지고 세 번째 단어의 확률을 예측하게 된다.
그렇게 계속 진행하면 마지막 \(\hat{y}^{<9>}\)의 output을 내보내고, 이 값은 EOS가 될 것이다.
이렇게 예측한 후에 Loss를 구하는데, 전체 Loss는 각 output의 Loss의 합이 된다.

세 개의 단어를 가지는 문장으로 정리해보자면, 첫 번째 단계에서 softmax output은 \(y^{<1>}\)의 확률을 알려주고, 두 번째는 이전 단어가 \(y^{<1>}\)일 때, \(y^{<2>}\)의 확률, 세 번째는 이전 단어가 \(y^{<1>}, y^{<2>}\)일 때, \(y^{<3>}\)의 확률을 알려주게 된다. 즉, \(P(y^{<1>}, y^{<2>}, y^{<3>}\)은 다음과 같다.
\[P(y^{<1>}, y^{<2>}, y^{<3>}) = P(y^{<1>}) P(y^{<2>}|y^{<1>}) P(y^{<3>}|y^{<1>}, y^{<2>})\]
조금 추상적인 내용이 될 수 있지만, 자세한 내용은 실습을 통해서 이해할 수 있을 것이다.
[Sampling novel sequences]
시퀀스 모델을 학습한 후에, 학습한 내용을 비공식적으로 파악할 수 있는 방법 중의 하나는 sample novel sequence를 갖는 것이다.

네트워크는 위와 같은 모델을 가지고 학습이 되었다.
그리고 sampling을 진행하는데, 샘플링의 과정은 다음과 같다.

\(a^{<0>}, x^{<1>}\)는 0 vector이고, 첫 번째로 softmax output \(\hat{y}^{<1>}\)를 출력한다. 이것은 각 단어의 확률이 얼마나 되는지 알려주는데, 이 벡터를 사용해서(numpy의 np.random.choice를 통해) 무작위로 첫 번째 단어를 샘플링 할 수 있다. 그런 다음 두 번째 단계로 넘어간다. 두 번째 단계에서는 샘플링한 값을 \(x^{<2>}\)로 사용한다.
이와 같은 과정을 계속 반복하는데, 예측값이 EOS Token이 될 때까지 샘플링을 반복하거나, 또는 정해진 샘플링 횟수를 정하고 그 단계에 도달할 때까지 계속하도록 할 수도 있다.
이것이 RNN 모델에서 무작위로 선택된 문장을 생성하는 방법이다.
지금까지 우리는 단어 수준의 RNN을 만들어 봤지만, 문자 수준의 RNN도 만들 수 있다.

즉, Training set는 개별 문자로 토큰화된다. (a, b, c, ..., A, B, C, ... 등으로)
문자 수준의 언어 모델을 사용하면 알 수 없는 단어에 대해 걱정할 필요가 없다.
하지만, 문자 수준은 입력이 훨씬 더 긴 배열로 이루어지기 때문에 문장의 초기 부분이 문장의 뒷부분에도 영향을 많이 줄 때의 성능이 단어 수준의 언어 모델보다 낮다.
다음은 실제 언어 모델의 사례이다.

뉴스 기사로 학습된 시퀀스 모델은 왼쪽과 같은 텍스트를 생성하고, 셰익스피어의 책에 의해 훈련된 모델은 셰익스피어가 쓴 것과 같은 텍스트를 생성한다.
[Vanishing gradients with RNNs]

Basic RNN 모델의 문제점 중의 하나는 Vanishing gradient 문제가 발생할 수 있다는 것이다.
아래와 같은 문장을 살펴보자.
'The cat, which already ate ...., was full'
'The cats, which already ate ...., were full'
이 예시는 문장의 단어가 긴 시간동안 의존성을 가지는 예시이다. 즉, 문장 초반부의 단어가 문장 후반부에 영향을 끼칠 수 있다는 것인데, RNN은 이와 같은 장기적인 의존성을 확인하는데 효과적이지 않다.
(긴 시퀀스를 처리하는데 한계가 존재함)
즉, cat나 cats처럼 단수/복수 명사가 문장 초반에 존재했다라는 것을 기억하고 있어야 제대로된 예측을 할 수 있는데, RNN의 경우에는 가까이에 있는 것에 영향을 더 많이 받는다. \(y^{<3>}\)은 \(y^{<3>}\)에 가까이 있는 값(입력)에 영향을 받는다.
이것이 Basic RNN 알고리즘의 약점이다.
(자세한 내용은 aikorea.org/blog/rnn-tutorial-3/ 참조)
Deep layer NN에 대해서 언급할 때, gradient가 기하급수적으로 감소해서는 안되고, 또한 기하급수적으로 증가해서도 안된다고 했었다. 여기서는 Vanishing gradient에 대해서 포커스를 맞추고 있지만, Exploding gradient가 최근 더 큰 문제로 대두되고 있는데, gradient가 너무 커져버리면, 네트워크의 매개 변수가 완전히 엉망이 되기 때문이다. 이 경우에는 gradient clipping을 통해서 어느 정도 해결할 수 있다.
다음 강의에서 Vanishing gradient를 해결하는 효과적인 해결책과 long-range dependency를 유지하는 방법에 대해서 알아보자.
'Coursera 강의 > Deep Learning' 카테고리의 다른 글
| [실습] Building a RNN step by step(Basic RNN, LSTM) (0) | 2020.12.21 |
|---|---|
| Recurrent Neural Networks 2 (GRU, LSTM, BRNN) (0) | 2020.12.21 |
| Neural Style Transfer (0) | 2020.12.01 |
| Face recognition (0) | 2020.11.30 |
| Object Detection(YOLO algorithm) (0) | 2020.11.22 |




댓글