References
- An Introduction to Parallel Programming
Contents
- 행렬-벡터 곱 연산 병렬화
- Cache, Cache Coherence, False Sharing
이전에 MPI를 통해서 행렬-벡터 곱 연산을 병렬화하고 그 성능을 평가해보았습니다.
2021.11.12 - [프로그래밍/병렬프로그래밍] - [MPI] 행렬 - 벡터 곱 연산 + 성능 평가
[MPI] 행렬 - 벡터 곱 연산 + 성능 평가
References An Introduction of Parallel Programming Contents 행렬 - 벡터 곱 연산 MPI_Allgather MPI_Wtime, MPI_Barrier 이번에는 행렬-벡터 곱 연산을 MPI를 사용하여 병렬화해보도록 하겠습니다. \(\text{A}..
junstar92.tistory.com
이번에는 Pthreads를 사용하여 행렬-벡터 곱셈 프로그램을 작성해보겠습니다.
\[A\textbf{x} = \textbf{y}\]
여기서 A = (\(a_{ij}\))는 m x n 매트릭스이고, \(\textbf{x} = (x_0, x_1, \cdots, x_{n-1})^T\)는 n차원의 열(columns) 벡터입니다. 따라서 \(A\textbf{x} = \textbf{y}\)는 m차원의 열 벡터가 됩니다. 잘 아시다시피 i번째 \(y_i\)는 아래의 연산으로 구할 수 있습니다.
\[y_i = \sum_{j=0}^{n-1}a_{ij}x_j\]
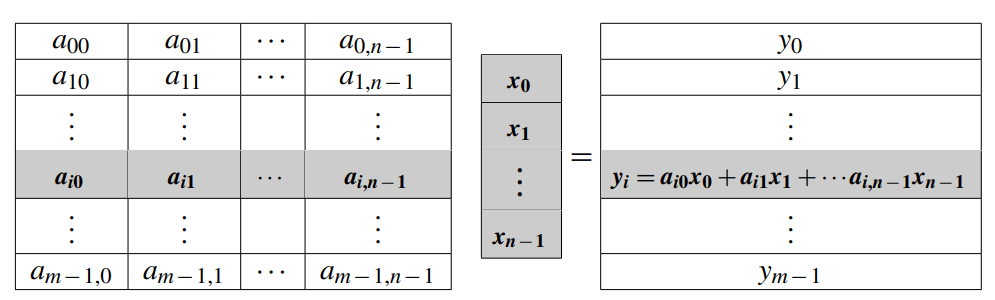
따라서, 위 연산은 아래의 코드로 표현할 수 있습니다.

시리얼로 행렬-벡터 곱셈은 이전 MPI 포스팅에서 다루었으므로, 여기서는 패스하도록 하겠습니다. 코드는 아래 링크 참조 바랍니다 !
https://github.com/junstar92/parallel_programming_study/blob/master/mpi/09_serial_mat_vec_mul_time.c
GitHub - junstar92/parallel_programming_study
Contribute to junstar92/parallel_programming_study development by creating an account on GitHub.
github.com
이제 이 코드를 스레드별로 일을 나누어서 병렬화 해보겠습니다. 한 가지 방법은 외부 루프를 스레드별로 분할할 수 있습니다. 이렇게 하면, 각 스레드는 y의 컴포넌트를 계산하게 됩니다. 예를 들어, m = n = 6이라고 하고, 스레드의 개수가 3이라고 가정해봅시다. 각 스레드별 연산은 다음과 같이 분할될 수 있습니다.

y[0]을 계산하기 위해서 스레드 0은 다음의 코드를 실행해야 합니다.

따라서, 스레드 0은 A의 0번째 행의 모든 요소와 x의 모든 요소에 액세스해야 합니다. 이걸 일반화하면, y[i]가 할당된 스레드에서는 다음의 코드를 실행하게 됩니다.

그러므로 이 스레드는 A의 i번째 행의 모든 요소와 x의 모든 요소에 액세스하게 됩니다. 각 스레드가 A의 일부 행과 y의 일부 컴포넌트에 액세스하는 반면, x는 각 스레드에서 모든 요소가 액세스 됩니다. 이는 x가 공유된다는 것을 의미하고 global로 x를 사용하면 됩니다. 그리고, A와 y 또한 편의와 효율을 위해서 global로 사용하도록 할 것입니다.
이제 각 스레드가 y의 컴포넌트를 계산하도록 코드를 작성해봅시다. 조금 심플하게 만들기 위해서 행렬의 각 차원 m과 n이 스레드 개수로 나누어 떨어진다고 가정하겠습니다. m = 6이고 스레드 개수 t = 3인 예시에서 각 스레드는 m/t개의 컴포넌트가 할당되게 됩니다. 스레드 0은 처음 m/t개의 컴포넌트를 할당받고, 스레드 1은 그 다음 m/t개의 컴포넌트를 할당받습니다. 따라서 스레드 q에 할당받는 첫 번째 컴포넌트는 다음과 같습니다.
\[\text{first component: } q \times \frac{m}{t}\]
그리고 마지막 컴포넌트는
\[\text{last component: } (q+1) \times \frac{m}{t} - 1\]
가 됩니다.
이 수식을 사용하여 행렬-벡터 곱셈을 수행하는 스레드 함수는 다음과 같이 작성할 수 있습니다. 코드에서 A, x, y, m, n은 global 변수이며 각 스레드에서 공유됩니다.
void* Pth_mat_vec_mul(void* rank)
{
long my_rank = (long)rank;
int local_m = m / thread_count;
int my_first_row = my_rank*local_m;
int my_last_row = my_first_row + local_m;
for (int i = my_first_row; i < my_last_row; i++) {
y[i] = 0.0;
for (int j = 0; j < n; j++) {
y[i] += A[i*n + j] * x[j];
}
}
return NULL;
}
그리고 main 함수를 다음과 같이 작성하고, 컴파일 후 실행해보도록 하겠습니다. 전체 코드는 아래 링크에서 확인하실 수 있습니다.
https://github.com/junstar92/parallel_programming_study/blob/master/pthread/01_pth_mat_vec_mul.c
GitHub - junstar92/parallel_programming_study
Contribute to junstar92/parallel_programming_study development by creating an account on GitHub.
github.com
#include <stdio.h>
#include <stdlib.h>
#include <pthread.h>
#include <time.h>
/* Global variables */
const int RMAX = 1000000;
int thread_count;
int m, n;
double *A, *x, *y;
void Generate_matrix(double mat[], int m, int n);
void Print_matrix(double mat[], int m, int n, char* title);
void Generate_vector(double vec[], int n);
void Print_vector(double vec[], int n, char* title);
void* Pth_mat_vec_mul(void* rank);
int main(int argc, char* argv[])
{
pthread_t* thread_handles;
if (argc != 4) {
fprintf(stderr, "usage: %s <thread_count> <m> <n>\n", argv[0]);
exit(0);
}
thread_count = strtol(argv[1], NULL, 10);
m = strtol(argv[2], NULL, 10);
n = strtol(argv[3], NULL, 10);
thread_handles = (pthread_t*)malloc(thread_count * sizeof(pthread_t));
A = (double*)malloc(m * n * sizeof(double));
x = (double*)malloc(n * sizeof(double));
y = (double*)malloc(m * sizeof(double));
Generate_matrix(A, m, n);
#ifdef DEBUG
Print_matrix(A, m, n, "A");
#endif
Generate_vector(x, n);
#ifdef DEBUG
Print_vector(x, n, "x");
#endif
clock_t start = clock();
for (long thread = 0; thread < thread_count; thread++)
pthread_create(&thread_handles[thread], NULL, Pth_mat_vec_mul, (void*)thread);
for (long thread = 0; thread < thread_count; thread++)
pthread_join(thread_handles[thread], NULL);
clock_t finish = clock();
#ifdef DEBUG
Print_vector(y, m, "y");
#endif
printf("Elasped time = %.6f seconds\n", (finish - start)/(double)CLOCKS_PER_SEC);
free(A);
free(x);
free(y);
free(thread_handles);
return 0;
}
컴파일 및 실행은 위의 커맨드로 하실 수 있습니다.
스레드의 개수를 증가시킬수록 실행 시간이 감소하는 경향은 있지만, 어느 정도의 편차가 존재하는 것 같습니다. 그리고 오히려 너무 많은 스레드를 사용하면 시간이 조금 증가하고 있습니다.
MPI 프로그래밍과 비교한다면, pthreads를 사용하면 더욱 쉽게 코드를 작성할 수 있는 것 같습니다. 특히 MPI 프로세스는 자신의 로컬 메모리만 직접 액세스할 수 있어, 각 프로세스의 메모리에 있는 x의 모든 요소들을 명시적으로 모아야했습니다. 행렬-벡터 곱셈에서 공유 메모리 프로그램이 분산 메모리 프로그램보다 더 쉽게 작성할 수 있었지만, 공유 메모리 프로그램이 더 복잡해지는 상황에서 발생할 수 있는 문제점들이 몇 가지 있습니다.
Cache, Cache Cogerence, False Sharing
프로세서가 발전되면서, 메인 메모리에 있는 데이터를 액세스하는 것보다 연산이 더욱 더 빨라졌습니다. 만약 프로세서가 메인 메모리로부터 데이터를 읽어와서 연산을 해야한다면, 프로세서는 메모리가 도착할 때까지 대부분의 시간을 대기하는데 사용할 것입니다. 이 문제를 해결하기 위해서 칩을 디자인하는 사람들은 상대적으로 빠른 메모리 block을 프로세서에 추가했습니다. 이 메모리 블럭을 cache memory(캐시 메모리)라고 합니다.
캐시 메모리의 디자인은 temporal and spartial locality 원칙을 고려합니다.
이 원칙은 만약 프로세서가 메인 메모리 위치 x를 t시간에 액세스 한다면, t에 가까운 시간에는 x에 가까운 위치의 메모리에 액세스할 것이라고 가정하는 것입니다. 따라서, 만약 프로세서가 메인 메모리 위치 x에 액세스할 때, 오직 x의 데이터만을 메인 메모리로부터 혹은 메인 메모리로 전송하기보다 x를 포함하는 메모리 블록을 프로세서의 캐시로 전송합니다. 이렇게 전송되는 블록은 cache line(캐시 라인) 혹은 cache block(캐시 블록)이라고 합니다.
CPU 캐시는 시스템 하드웨어에 의해서 관리되며, 프로그래머가 직접 캐시를 제어할 수는 없습니다. 이 때문에 문제가 발생하는데, 이 문제를 이해하기 위해서 두 개의 스레드가 공유 변수 x에 접근하여 수행하는 예시를 살펴보겠습니다.
x가 5라는 값을 갖는 공유 변수라고 할 때, 스레드 0과 스레드 1은 메인 메모리에서 x를 각각의 캐시로 읽어옵니다. 그리고 이 두 스레드는 아래의 문장을 실행합니다.
my_y = x;my_y는 각 스레드에서 정의된 private 변수이며, 공유 변수를 읽기만 한다면 여기까지는 문제가 없습니다.
하지만 스레드 0은 다음 문장을 실행하고,
x++;이 다음에 스레드 1은 다음 문장을 실행한다고 가정해봅시다. my_z는 스레드 1의 다른 private 변수입니다.
my_z = x;여기서 my_z에 저장된 값은 무엇일까요? 5 ? 아니면 6일까요?
여기서 문제는 이 프로그램에 x의 복사본이 3개가 있다는 점입니다. 메인 메모리에 하나, 스레드 0의 캐시에 하나, 그리고 스레드 1의 캐시에 하나가 있습니다. 스레드 0이 x++을 실행할 때 메인 메모리에 있는 값과 스레드 1의 캐시에는 어떤 일이 발생할까요?
메인 메모리와 캐시의 데이터 불일치가 발생할 수 있고, 데이터 불일치를 없애는 것을 캐시 일관성을 유지한다라고 합니다. 캐시 일관성을 보장하기 위해서 스누핑(snooping)과 디렉토리 기반 캐시 일관성(directory-based cache coherence)라는 방법이 있습니다. 이 포스팅에서 자세한 설명은 패스하도록 하겠습니다.
대부분의 시스템에서 캐시는 캐시하는 데이터의 변화를 캐치하도록 되어 있습니다. 스레드 0에서 x++이 수행되고, 스레드 1의 my_z = x가 수행되기 전에 스레드 1의 캐시에 있는 라인은 invalid 로 표시되어 스레드 1에서 실행되는 코어가 현재 x의 데이터가 쓸모없다는 것을 알게 됩니다. 그러므로, 스레드 0이 실행되는 코어는 메인 메모리에서 x의 카피(현재보다 조금 전인)를 업데이트하고, 스레드 1을 실행하는 코어는 메인 메모리에서 업데이트된 x를 얻는 라인이 추가됩니다.
이러한 캐시 일관성의 사용은 공유 메모리 시스템에서의 성능에 큰 영향을 미칩니다. 위의 행렬-벡터 곱셈 프로그램에서 메인 스레드는 m x n 행렬 A과 n차원의 벡터 x를 초기화하고, 각 스레드는 y = Ax를 계산합니다. 여기서 A, x, y, m, n은 모두 공유됩니다.
행렬의 크기를 8,000,000 x 8 , 8,000 x 8,000 , 8 x 8,000,000 으로 변경해가며 각 스레드별 수행 시간을 측정한 결과입니다. 단위는 초입니다.
| 스레드 | 행렬 크기 | ||
| 8,000,000 x 8 | 8,000 x 8,000 | 8 x 8,000,000 | |
| 1 | 0.174 | 0.158 | 0.171 |
| 2 | 0.088 | 0.081 | 0.168 |
| 4 | 0.048 | 0.041 | 0.134 |
실행할 때마다 다르기 때문에 약간의 오차는 있습니다.
for (int i = my_first_row; i < my_last_row; i++) {
y[i] = 0.0;
for (int j = 0; j < n; j++) {
y[i] += A[i*n + j] * x[j];
}
}이 실행 시간의 차이점은 적어도 부분적으로는 캐시 성능에 좌우됩니다.
코어가 캐시에 없는 변수를 업데이트할 때 write-miss가 발생하며, 메인 메모리에 액세스해야 합니다. 그리고 코어가 캐시에 없는 변수를 읽어 올때 read-miss가 발생하고, 메인 메모리에 액세스하여 읽어옵니다.
valgrind를 실행하면, 8,000,000 x 8 에서의 cache miss를 어느정도 프로파일링할 수 있습니다.
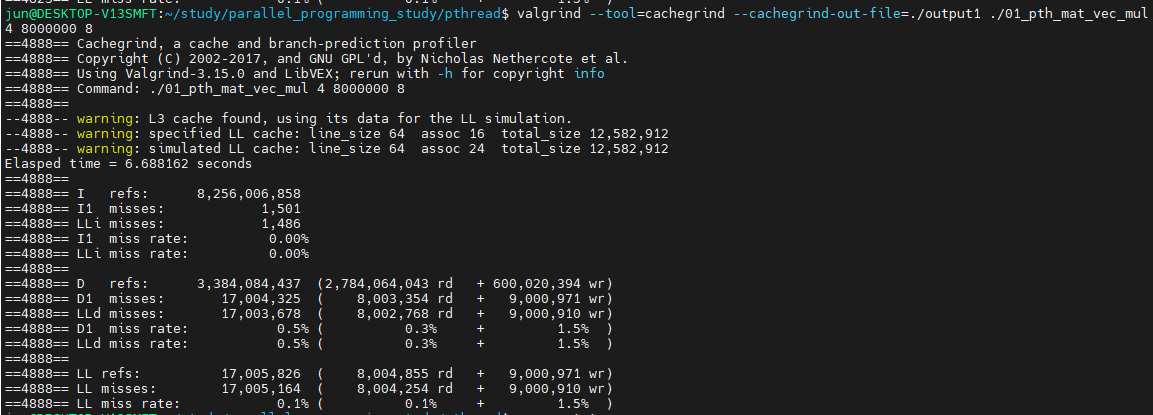
첫 번째 I refs는 명령어를 읽을 때의 cache miss 발생량과 발생률입니다.
두 번째 D refs는 데이터를 읽고 쓸 때의 cache miss 발생량과 발생률이며, 마지막 LL refs는 데이터를 읽고 쓸 때, Last-Level 캐시에서의 cache miss 발생량과 발생률입니다.
정리된 결과를 valgrind의 --cachegrind-out-file 옵션으로 저장할 수 있고, 이 결과는 cg_annotate로 확인할 수 있습니다.

Ir은 명령어 캐시 read이고, I1mr는 I1 cache read misses, ILmr은 LL cache instruction read misses 입니다.
우리가 중점적으로 살펴볼 건 데이터를 읽고 쓸 때의 cache miss 이므로, D1mr, DLmr, D1mw, DLmw를 살펴봐야합니다.
D1mr은 D1 cache read misses, DLmr은 LL cache data read misses를 의미합니다. r대신 w가 붙은건 write misses입니다.
중간에 있는 표는 프로그램 전체에서의 cache 프로파일링 결과이며, 아래 표는 프로그램 내 함수별 cache 프로파일링 결과입니다. 아래에 있는 표에서 첫 번째 결과 라인이 우리가 관심있는 Pth_mat_vec_mul 함수에서의 cache miss 결과입니다. 그리고 cg_annotate로 결과를 출력할 때, --auto=yes 옵션을 추가해서 실행하면, 라인별로 cache miss를 확인할 수 있습니다.

편하게 보기 위해서 전체 결과를 잘랐는데, 왼쪽부터 D1mr, DLmr, Dw, D1mw, DLmv 입니다. read misses와 write misses를 중점적으로 살펴보겠습니다.
4개의 스레드로 8,000 x 8,000 행렬 곱셈의 결과는

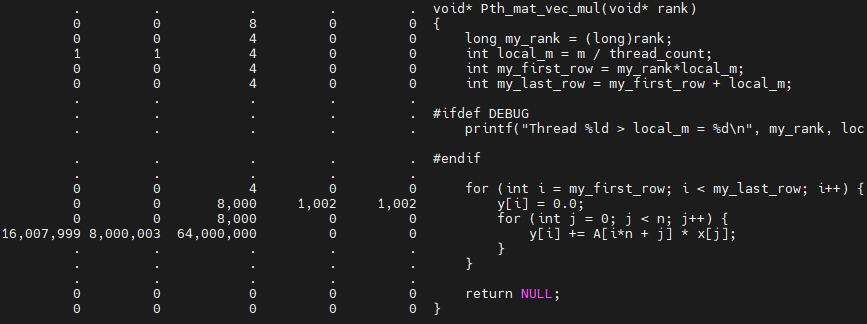
입니다. 8,000,000 x 8 행렬보다 D1 read miss는 증가했지만, D1,DL의 write miss는 매우 감소했다는 것을 볼 수 있습니다.
8 x 8,000,000 행렬의 결과는
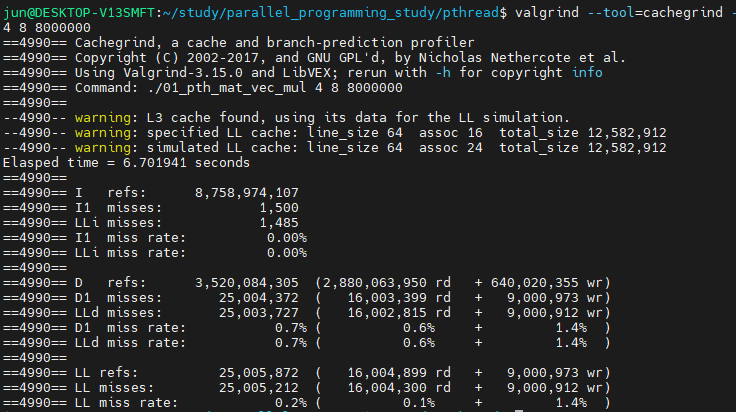

입니다.
결과를 정리하면,
| 8,000,000 x 8 | 8,000 x 8,000 | 8 x 8,000,000 | |
| D1mr | 8,000,003 | 16,007,999 | 16,000,012 |
| DLmr | 8,000,003 | 8,000,003 | 16,000,012 |
| D1mw | 1,000,003 | 1,002 | 3 |
| DLmw | 1,000,003 | 1,002 | 3 |
세 가지 테스트 중에서 8,000,000 x 8 행렬에서 write-miss 비중이 가장 크고, 8 x 8,000,000 행렬은 read-miss 비중이 크다는 것을 볼 수 있습니다.
조금 흥미로운 점은 8 x 8,000,000 크기의 행렬에서는 스레드의 개수가 많아져도 다른 행렬 크기만큼 수행 속도가 크게 향상되지 않는다는 점입니다. 이 현상의 원인도 캐시인데, 테스트한 것처럼 4개의 스레드로 프로그램을 실행했다고 가정해봅시다. 8,000,000 x 8 입력은 각 스레드는 y를 2,000,000개씩 할당받습니다. 8,000 x 8,000의 경우에는 각 스레드가 y를 2,000개씩 할당받고, 8 x 8,000,000는 각 스레드가 y를 2개씩 할당받습니다.
제 노트북의 캐시 라인은 64바이트이고, y의 타입은 double, 즉 8바이트입니다. 따라서 하나의 캐시 라인에는 8개의 double형을 저장할 수 있습니다.
캐시 일관성은 'cache-line level'에 따라 동작합니다. 즉, 캐시 라인에 매번 어떠한 값이 쓰여질 때마다, 이 라인이 다른 프로세서의 캐시에 존재한다면, 전체 캐시 라인이 invalidated됩니다. 스레드 0과 스레드 1이 하나의 프로세서에 할당되고 나머지 스레드가 다른 프로세서에 할당되었다고 가정해봅시다. 또한, 8 x 8,000,000 입력에서 y 전체가 각 싱글 캐시라인에 저장되었다고 가정해봅시다. (캐시 라인이 64바이트이므로, y[8]을 모두 캐시 라인에 저장한 경우입니다.)
그렇다면, y의 요소에 어떠한 값을 쓸때마다 다른 프로세서 캐시의 라인은 invalidated 됩니다. 예를 들어, 스레드 0이 매번 아래 코드에서 y[0]을 업데이트하는 경우,
y[i] += A[i][j]*x[j];만약 스레드 2 혹은 3이 위의 코드를 실행한다면, y를 다시 로드해야 합니다. 각 스레드는 할당받은 y의 요소를 8,000,000번 업데이트합니다. 2개씩 할당받았기 때문에 각 스레드에서는 총 16,000,000번의 업데이트가 발생합니다. 따라서 각 스레드가 모두 동일한 y를 캐시 라인에 저장하고 있기 때문에 y값을 업데이트할 때마다 각 스레드는 y를 계속해서 다시 로드하게 되는 것입니다.
즉, 스레드들이 같은 변수를 공유하는 것은 아니지만 같은 캐시 라인에 속한 다른 변수를 액세스하게 되고, 이를 거짓 공유(false sharing)이라고 합니다. 스레드는 어떤 변수(캐시 라인 제외)도 공유하고 있지 않지만 메모리 액세스에 대한 스레드의 동작은 그 스레드들이 변수를 공유하고 있는 것처럼 동작합니다.
약간 횡설수설로 설명한 것 같긴합니다만... 캐시와 캐시 일관성에 대해서 약간이나마 설명이 되었으면 좋겠습니다. 기회가 된다면 캐시에 관해서는 조금 더 자세하게 공부하고, 다시 포스팅하도록 하겠습니다.
다음 포스팅에서 공유 메모리 프로그램에서 발생할 수 있는 다른 문제점과 그 문제점을 어떻게 해결하는지 알아보도록 하겠습니다 !
'프로그래밍 > 병렬프로그래밍' 카테고리의 다른 글
| [pthread] Thread 동기화 (0) | 2021.11.18 |
|---|---|
| [pthread] Critical Section (0) | 2021.11.17 |
| [pthread] Hello, Pthreads (0) | 2021.11.15 |
| [MPI] Odd-even transposition sort (MPI Safety) (0) | 2021.11.13 |
| [MPI] MPI Derived Datatypes (파생 데이터타입) (0) | 2021.11.13 |




댓글