References
- 리얼월드 알고리즘
Contents
- LZW 인코딩/디코딩 과정
- LZW 디코딩에서 코너 케이스
- C++ 구현
지난 글에서 다루었던 허프만 코딩은 압축하고자하는 아이템의 빈도에 따라서 인코딩의 길이를 다르게하여 압축하는 방식이었습니다.
2021.08.05 - [Data Structure & Algorithm/알고리즘] - 허프만 코딩 (C++ 구현)
허프만 코딩 (C++ 구현)
References 리얼월드 알고리즘 허프만 코딩 허프만 코드는 (최소)우선순위 큐와 이진 트리로 만들 수 있는 유일 접두어 코드를 의미합니다. 1951년 데이비드 허프만(David A. Huffman)이 25살 때 고안한 방
junstar92.tistory.com
즉, 자주 나오는 아이템의 경우에는 짧은 인코딩으로 압축하고, 빈도가 낮은 아이템은 긴 인코딩으로 압축하는 것이죠.
이번에 알아볼 LZW 압축은 인코딩 길이에 변화가 아닌 인코딩당하는 아이템의 길이를 변경하여 압축하게 됩니다.
아스키로 인코딩된 텍스트가 있다고 가정해보겠습니다. 이 경우에는 문자당 7비트가 필요합니다.

그렇다면 아스키로 인코딩하는 방식에서 조금 더 나아가서, 인코딩하는데 더 많은 비트를 사용하기로 해봅시다.
즉, 7비트가 아닌 8비트로 아이템(여기서는 텍스트)을 인코딩하는 것입니다.
8비트를 사용하게 된다면, \(2^8\) = 256가지 아이템을 표현할 수 있습니다.
따라서, 0x00(0u)부터 0x7F(127)까지의 숫자는 기존과 동일하게 아스키 문자를 표현하는 데 사용하고, 0x80(128)부터 0xFF(255)까지의 숫자는 원하는 것을 표현하는데 사용하게 됩니다.
여기서 우리는 아스키 코드를 제외한 나머지 128개 숫자를 한 개의 문자 대신에 둘, 셋 또는 그 이상의 문자열을 표현하는데 사용할 것입니다.
하나의 문자로 구성된 문자열은 유니그램(unigram), 두 개 문자로 구성된 문자열을 바이그램(bigram)이라 하고, 세 개의 문자로 구성된 문자열을 트라이그램(trigram)이라고 합니다. 이보다 더 긴 문자열은 구성하는 문자의 수에 그램(gram)이라는 접미사를 붙여서 부르고, 일반적으로 n-gram이라고 합니다.
그래서 0부터 127까지는 유니그램을 표현하는데 사용하고, 128부터 255까지는 유니그램이 아닌 1보다 큰 n-gram을 나타내는데 사용합니다.
그렇다면, 8비트로 아이템을 인코딩한다면 우리는 어떤 n-gram을 사용하게 될까요?
사실, LZW 압축에서 어떤 n-gram을 사용할 지는 압축하고자하는 텍스트를 실제 인코딩하기 전까지는 알 수 없습니다.
26개의 알파벳으로 \(26^2 = 676\)개의 바이그램이 가능하고, \(26^3 = 17,576\)개의 트라이그램, 임의의 n으로는 \(26^n\)의 n-gram이 가능합니다. LZW 압축은 이 중에서 일부인 작은 부분 집합을 선택하게 됩니다.
다시 말하자면, LZW 압축은 압축하려는 텍스트를 훑어가며 n-gram을 찾아가면서 인코딩을 구성한다는 것을 의미합니다.
LZW 압축
LZW 압축이 어떻게 진행되는 지 예시를 통해서 살펴보겠습니다.
예시로 'MELLOW YELLOW FELLOW'를 사용할 것입니다. 그리고 앞서 언급했듯이 8비트를 사용하여 n-gram을 구성하도록 할 것이고, 하위 7비트는 단일 문자들의 아스키 인코딩에 해당합니다. 인코딩은 문자와 값을 매핑한 테이블을 사용하도록 표시하도록 하겠습니다. (아스키 코드는 미리 매핑 테이블에 추가해두게 됩니다.)

LZW 압축은 압축하고자하는 문자열을 처음부터 읽으면서 인코딩을 진행합니다. 빨간색 박스는 현재 위치의 문자를 의미합니다.

먼저 압축하고자하는 문자열의 첫 번째 문자인 유니그램 문자 'M'을 읽고 매핑 테이블에 있는지 확인해봅니다. 'M'은 당연히 아스키 코드에 존재하기 때문에 매핑 테이블에 존재합니다. 이때 M에 해당되는 값을 바로 인코딩하는 것이 아니라, 더 긴 n-gram이 있는지 알아봅니다.
(지금은 테이블에 유니그램보다 더 긴 n-gram이 없습니다만, 전반적인 로직의 일관성을 위해서 처음에도 적용됩니다.)
그리고 다음 문자인 'E'를 읽습니다.(그림의 두 번째 줄)
이제 바이그램인 'ME'가 테이블에 존재하는지 확인합니다. 그림에서 매핑 테이블에 존재하는 n-gram 부분을 붉은색으로 음영처리 하였습니다.
'ME'는 테이블에 없는데, 그러면 테이블에 있는 'M'의 n-gram 값 77을 인코딩하고, 새로운 바이그램인 'ME'를 테이블에 넣어 사용이 가능한 다음 값 128을 할당합니다. 즉, 다음에 'ME'를 만나게 되면 두 문자를 나타내는 128로 인코딩될 것입니다.
(그림의 왼쪽 인코딩 부분이 실제 인코딩되는 과정, 즉, M이 77로 인코딩됨을 보여주고, 오른쪽 부분은 테이블에 삽입되는 내용을 보여줍니다.)
이제 'M'의 인코딩 값을 출력했으므로, 이제 이 n-gram은 필요없게 되고, 마지막으로 읽은 글자인 'E'를 다음 n-gram의 시작으로 사용합니다. 처음 단계와 같이 'E'는 매핑 테이블에 존재하는 유니그램이지만, 다음 단계에서 'E'로 시작하는 더 긴 n-gram을 찾도록 합니다.

따라서 다음 단계에서 문자 'L'을 읽고 'E'를 확장하여 바이그램 'EL'을 생성합니다. 'EL'은 테이블에 존재하지 않으므로, 'E'에 대한 값인 69로 인코딩하고 'EL'을 값 129와 함께 테이블에 삽입한 뒤에 다음 n-gram의 시작 문자로 'L'을 유지합니다.

위 그림은 'MELLOW'의 압축 과정을 보여주고 있습니다. 앞서 설명한 과정을 계속해서 반복하면서 인코딩을 진행합니다. 공백을 만났을 때에도 같은 방법을 계속 적용하며, 바이그램 'W_'는 테이블에 없으므로 'W'를 인코딩(87)하고, 'W_'와 인코딩 값인 133을 테이블에 삽입합니다.

같은 방법으로 인코딩을 계속 진행하다보면, (위 그림 세 번째 줄)'YELLOW'의 첫 번째 L 위치에서 'EL'이 이미 테이블에 존재한다는 것을 발견하게 됩니다. 그래서 문자를 하나 더 취하여 n-gram의 확장을 시도하고자 두 번째 L을 읽습니다. 따라서 그림의 네 번째 줄에서 테이블에 존재하지 않는 새로운 트라이그램인 'ELL'을 만들고 그 값인 136과 함께 테이블에 삽입합니다. 그런 다음 이전 n-gram인 바이그램 'EL'을 인코딩(129)하고, 마지막으로 읽은 문자 'L'로 새로운 n-gram을 시작합니다.
나머지 과정은 다음과 같습니다.

'MELLOW YELLOW FELLOW'를 LZW 압축하게 되면,
압축 결과는 '77 69 76 76 79 87 32 89 129 131 133 70 136 132'로 얻을 수 있습니다.
전반적인 로직은 다음과 같습니다.
1. 문자를 읽는다.
2. 읽은 문자로 현재의 n-gram을 확장한다.
3-1. 만들어진 n-gram이 테이블에 있으면, 1로 돌아가서 반복
3-2. 테이블에 없다면, 만들어진 n-gram을 테이블에 삽입하고, 이전 n-gram의 코드 값을 인코딩
4. 방금 읽은 문자를 현재 n-gram으로 설정하고, 1로 돌아가서 반복
간단히 말하자면, 가능한 가장 긴 n-gram으로 인코딩을 시도합니다. 이전에 보지 못했던 n-gram을 만날 때마다 새로운 n-gram에 코드를 할당하여 다음에 해당 n-gram을 만날 때 사용할 수 있도록 합니다. 텍스트 압축을 진행하면서 여러 번 나타날 수 있는 n-gram을 인코딩하게 되므로 원본 텍스트를 표현하는데 필요한 공간을 절약할 수 있습니다.
이 예시에서 사용한 문자열은 20개의 문자로 구성되므로 아스키 코드로 표현하면(7비트 압축), \(20 x 7 = 140\)비트가 필요합니다. 하지만 8비트를 사용하는 LZW를 이용하면 이 문자열은 8비트로 표현되는 14개의 숫자 [77, 69, 76, 76, 79, 87, 32, 89, 129, 131, 133, 70, 136, 132]로 인코딩됩니다. 따라서, \(14 x 8 = 112\)비트가 필요하게 되므로, 원래 크기의 80%로 구문이 압축됩니다.
물론 이 예시는 보여주기 위해서 짧고, 반복되는 n-gram을 표현하기 위한 예시라는 점을 고려하면 80%가 그리 인상적인 효과는 아닙니다. 하지만 실제 프로그램에서는 8비트가 아닌 더 큰 비트를 사용하여 더 많은 알파벳과 n-gram을 수용할 수 있도록 할 수 있습니다. 만약 인코딩에 12비트를 사용한다면 총 4095까지의 값으로 n-gram을 나타낼 수 있고, 텍스트가 길어지면 n-gram을 반복할 기회가 더 많아지고 n-gram은 더 길어질 것입니다.
(제임스 조이스의 율리시스라는 책을 이러한 방법으로 압축하면 텍스트가 원래 크기의 53%로 압축됩니다.)
LZW 압축 해제
LZW로 압축된 메세지의 압축을 풀려면 인코딩 과정을 역으로 따르면 됩니다. 일련의 인코딩 문자열이 주어지고 인코딩되기 전의 원본 텍스트를 얻고자 할 때 시작 부분에서는 유니그램(아스키 코드)을 위한 인코딩을 제외하고는 어떤 n-gram이 어떤 방식으로 인코딩되었는지 모릅니다.
따라서 LZW의 압축 해제는 압축 과정의 시작부터 사용한 원래 테이블의 역 해석 과정입니다.
위에서 LZW의 압축 과정을 살펴보면 문자를 인코딩할 때마다 다음에 읽은 문자로 n-gram을 생성하고 있음을 볼 수 있습니다. 압축된 메세지를 가지고 역으로 인코딩 테이블을 재구성하려면 읽은 인코딩 값을 기록하고, 다음 인코딩 값을 읽고 이 값(다음 인코딩 값)의 디코딩 값을 찾은 뒤, 이전 출력과 방금 찾은 디코딩 값의 첫 번째 문자로 구성된 n-gram을 테이블에 삽입해야 합니다.
위에서 'MELLOW YELLOW FELLOW'의 디코딩 값 '77 69 76 76 79 87 32 89 129 131 133 70 136 132'의 디코딩 과정을 그림으로 살펴보겠습니다. 이제 우리가 찾아야하는 인코딩 테이블은 문자 -> 인코딩 값으로 매핑되는 테이블입니다.


첫 번째 인코딩 값에서는 오직 유니그램(아스키 코드)만 있으므로 다른 할 일이 없고, 인코딩 값을 읽은 뒤에 디코딩 테이블에서 변환 값(M)을 찾으면 됩니다. 그리고 두 번째 인코딩부터는 이전 변환 값(M)과 현재 변환 값(E)의 첫 번째 문자(E)로 구성된 n-gram을 디코딩 테이블에 삽입해야 합니다. 이러한 방식으로 디코딩 테이블은 인코딩 값들을 따라가면서 채워지게 되는데, 첫 번째로 만나는 바이그램인 129를 읽으면 세 번째 줄에서 디코딩 테이블에 삽입한 내용을 성공적으로 읽어서 디코딩할 수 있게 됩니다.
디코딩 과정에서의 코너 케이스
하지만, 위의 디코딩 과정에는 문제가 하나 있습니다.
현재 압축된 인코딩 값을 항상 따라가면서 디코딩 테이블에서 인코딩 값을 항상 찾을 수 있을까요?
이 예에서 인코딩하면서 추가된 값들은 전부 사용되기 여러 단계 전에서 인코딩 테이블에 입력되었습니다. 하지만 압축하는 과정 중에 생성된 n-gram이 바로 다음 단계에서 사용된다면 어떻게 될까요?
이것이 바로 LZW 인코딩/디코딩의 코너 케이스(Coner Case)의 한 예입니다.
문자열 'ABABABA'를 압축하는 과정을 살펴보겠습니다.

LZW 압축 해제에서 코너 케이스는 압축 중에 n-gram을 생성하고 그 다음 단계에서 그 값을 인코딩할 때 발생합니다. 그 과정이 위의 ABABABA의 인코딩 과정 중에 발생합니다. 문자열 'ABABABA'를 압축하는데 'AB'를 인코딩하고 다음에 'BA', 그 다음에 'ABA'를 인코딩 합니다. 이때 'ABA'는 인코딩 테이블에 삽입된 뒤에 바로 다음 인코딩 단계에서 사용됩니다.
이렇게 ABABABA가 압축되면 [65, 66, 128, 130]이 되고, 이제 이 값을 압축 해제해보도록 하겠습니다.

압축 해제할 인코딩 값이 주어지면, 디코딩 테이블에 대응하는 값인 'A'에 대응하는 65부터 시작하게 됩니다. 그 다음에 'B'로 인코딩된 숫자 66을 사용합니다. 그리고 디코딩 테이블에 값 128을 갖는 'AB'를 추가하고 다음으로 압축 해제할 값은 128을 디코딩 테이블에서 읽어서 'AB'로 디코딩하게 됩니다. 마지막으로 130을 디코딩 테이블에서 검색하는데, 130은 아직 디코딩 테이블에 입력되지 않았기 때문에 여기서부터 문제가 됩니다.
이것을 어떻게 해결할 수 있을지 알아보려면 인코딩 과정에서 무언가를 인코딩하고 그 인코딩을 바로 다음 단계에서 사용할 때 코너 케이스가 발생한다는 것을 기억해야 합니다.
예를 들어서 인코딩 과정에서 문자열 x[0]x[1]...x[k]를 읽고 이것을 인코딩 테이블에서 찾았고, 그 다음 x[k+1]을 읽고 x[0]x[1]...x[k]x[k+1]를 테이블에서 찾지 못하여 새로운 인코딩을 추가했다고 가정해보겠습니다. 그리고 다음 인코딩하는 문자열이 정확하게 x[0]x[1]...x[k]x[k+1]일 때 코너 케이스가 발생합니다.
즉, x[0] = x[k+1]이고 새로 생성된 n-gram은 첫 번째 문자가 이전 n-gram의 끝에 붙어 있는 것과 같습니다.
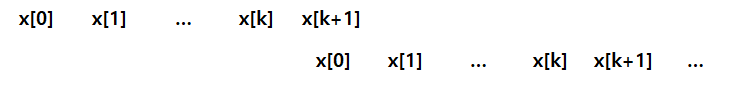
따라서 이 문제를 해결하기 위해서는 디코딩 테이블에 아직 삽입되지 않은 인코딩 값을 만난다면 마지막 n-gram에 첫 번째 문자를 추가하여 생성한 n-gram을 키로 하는 새로운 엔트리를 디코딩 테이블에 입력해야 합니다.
위 예에서 130을 읽었을 때 이 값은 디코딩 테이블에 존재하지 않습니다. 따라서, 130을 읽기 전에 디코딩 테이블에 'AB'를 넣었고, 'AB'에 'A'를 추가하여 'ABA'를 생성하고 이를 디코딩 테이블에 삽입합니다. 이렇게 130을 읽기 전에 이 작업을 수행해주면 { 130 : ABA }를 디코딩 테이블에 추가하여 성공적으로 130을 디코딩 할 수 있습니다.
C++ 구현
LZW를 C++로 구현해봤습니다. (펼치기 확인)
#ifndef __LZW_HPP__
#define __LZW_HPP__
#include <string>
#include <list>
#include <unordered_map>
#include <iostream>
#include <type_traits>
template <size_t _Bits>
class LZW {
using _Ty = std::conditional_t<_Bits <= sizeof(unsigned long) * CHAR_BIT,
std::conditional_t<_Bits <= sizeof(unsigned char), unsigned char, unsigned long>, unsigned long long>;
private:
size_t bits;
_Ty max_code;
void print(std::list<_Ty> compressed) {
for (auto& val : compressed) {
std::cout << val << " ";
}
std::cout << "\n";
}
public:
LZW() {
bits = _Bits;
if (bits > sizeof(unsigned long long) * CHAR_BIT)
{
bits = sizeof(unsigned long long) * CHAR_BIT;
std::cout << "bit size is changed to " << bits << "\n";
}
max_code = (_Ty{ 1 } << bits) - 1;
}
std::list<_Ty> compress(std::string input) {
std::cout << "input string : " << input << "\n";
std::unordered_map<std::string, _Ty> table;
_Ty code = _Ty{ 128 };
for (char i = 0; i < code; i++) {
std::string tmp(1, i);
table[tmp] = i;
}
std::list<_Ty> compressed;
std::string w = "";
for (auto& c : input) {
std::string wc = w + c;
if (table.find(wc) != table.end()) {
w = wc;
}
else {
compressed.push_back(table[w]);
w = c;
if (code > max_code) {
std::cout << "max_code overflow!\n";
compressed.clear();
return compressed;
}
table[wc] = code;
code += 1;
}
}
if (w != "") {
compressed.push_back(table[w]);
}
std::cout << "Compression Fishished : ";
print(compressed);
return compressed;
}
std::string decompress(std::list<_Ty> compressed) {
std::unordered_map<_Ty, std::string> table;
_Ty code = 128;
for (char i = 0; i < code; i++) {
std::string tmp(1, i);
table[i] = tmp;
}
std::string v = table[compressed.front()];
compressed.pop_front();
std::string decompressed = "";
decompressed += v;
std::string pv = v;
for (auto& c : compressed) {
if (table.find(c) == table.end()) {
v = pv + pv[0];
}
else {
v = table[c];
}
decompressed += v;
if (code > max_code) {
std::cout << "max_code overflow!\n";
return "";
}
table[code] = pv + v[0];
code += 1;
pv = v;
}
std::cout << "Decompression Finished : " << decompressed << "\n";
return decompressed;
}
};
#endif
먼저 template 부터 살펴보면, 사용할 bits 크기를 템플릿 인자로 받습니다. 이렇게 받은 bits 크기는 인코딩/디코딩 과정에서 사용되는 테이블에서 인코딩 값을 담는 자료형을 결정하게 됩니다. 딱, 사용하는 비트 수 크기만큼의 자료형을 찾다가 std::bitset을 발견했지만, 실제 차지하는 크기는 비트 수 만큼이 아니여서 아쉽지만 입력받은 비트 수를 포함하는 자료형으로 사용하도록만 설정했습니다.
다음은 압축을 위한 함수입니다.
압축할 동안 사용할 table은 unordered_map을 사용했으며, key는 string, value는 인코딩에 사용될 자료형인 _Ty 입니다. 인코딩을 시작하기 전에 유니그램인 아스키코드는 기본적으로 입력해놓고 인코딩을 시작하게 됩니다.
compressed는 인코딩된 값들을 저장하는 list 이며, w는 현재의 n-gram, code는 다음 인코딩 테이블에 삽입될 값을 의미합니다.
압축 과정은 위에서 설명한 것과 동일합니다. 아마 보시면 쉽게 이해하실 거라고 생각합니다.
압축이 완료되면 인코딩 값들의 리스트를 반환합니다.
std::list<_Ty> compress(std::string input) {
std::cout << "input string : " << input << "\n";
std::unordered_map<std::string, _Ty> table;
_Ty code = _Ty{ 128 };
for (char i = 0; i < code; i++) {
std::string tmp(1, i);
table[tmp] = i;
}
std::list<_Ty> compressed;
std::string w = "";
for (auto& c : input) {
std::string wc = w + c;
if (table.find(wc) != table.end()) {
w = wc;
}
else {
compressed.push_back(table[w]);
w = c;
if (code > max_code) {
std::cout << "max_code overflow!\n";
compressed.clear();
return compressed;
}
table[wc] = code;
code += 1;
}
}
if (w != "") {
compressed.push_back(table[w]);
}
std::cout << "Compression Fishished : ";
print(compressed);
return compressed;
}
다음은 디코딩 함수입니다. 앞서 설명대로 인코딩 테이블을 찾아가는 역 과정이며, table은 key가 인코딩 값, value가 string이 됩니다. 파라미터로 압축된 인코딩 list를 입력받습니다. 여기서 pv는 이전 n-gram을 의미하고, decompressed는 디코딩된 문자들을 저장하는 문자열입니다. v는 임시로 문자열을 저장하는데 사용됩니다.
디코딩 과정은 10 line부터 시작되는데, 디코딩의 첫 번째 과정은 항상 유니그램이기 때문에 그냥 디코딩 테이블에서 찾을 수 있습니다.
그리고 다음 인코딩 값부터 순서대로 탐색하며 디코딩을 진행하는데, 코너 케이스 때문에 현재 인코딩 값이 테이블에 존재하는지 먼저 확인하고 진행합니다. 인코딩 값이 존재하지 않는다면 이전 n-gram에 n-gram 첫 번째 문자를 추가한 n-gram을 디코딩 결과에 추가(line 20~24)하고, 존재한다면(line 17~19) 디코딩 테이블의 값을 디코딩 결과에 추가합니다.
그리고 이전 n-gram에 현재 디코딩된 문자열의 첫 번째 문자를 합쳐서 디코딩 테이블에 삽입합니다.
위 과정을 모든 인코딩 값을 탐색할 때까지 반복하게 됩니다.
std::string decompress(std::list<_Ty> compressed) {
std::unordered_map<_Ty, std::string> table;
_Ty code = 128;
for (char i = 0; i < code; i++) {
std::string tmp(1, i);
table[i] = tmp;
}
std::string v = table[compressed.front()];
compressed.pop_front();
std::string decompressed = "";
decompressed += v;
std::string pv = v;
for (auto& c : compressed) {
if (table.find(c) == table.end()) {
v = pv + pv[0];
}
else {
v = table[c];
}
decompressed += v;
if (code > max_code) {
std::cout << "max_code overflow!\n";
return "";
}
table[code] = pv + v[0];
code += 1;
pv = v;
}
std::cout << "Decompression Finished : " << decompressed << "\n";
return decompressed;
}
실제 돌려본 결과입니다.
int main(void) {
LZW<8> lzw;
auto result = lzw.compress("MELLOW YELLOW FELLOW");
lzw.decompress(result);
result = lzw.compress("ABABABA");
lzw.decompress(result);
return 0;
}
https://github.com/junstar92/DataStructure_Algorithm/tree/master/Algorithm/LZW
GitHub - junstar92/DataStructure_Algorithm
Contribute to junstar92/DataStructure_Algorithm development by creating an account on GitHub.
github.com
'Data Structure & Algorithm > 알고리즘' 카테고리의 다른 글
| [암호] AES (C++ 구현/멤버 변수, public 함수) - 2 (0) | 2021.09.23 |
|---|---|
| [암호] AES (Advanced Encryption Standard) - 1 (0) | 2021.09.23 |
| 허프만 코딩 (C++ 구현) (8) | 2021.08.05 |
| Rabin-karp(라빈 카프) 알고리즘 (0) | 2020.12.17 |
| KMP 알고리즘 (0) | 2020.11.25 |




댓글