해당 내용은 Andrew Ng 교수님의 Machine Learning 강의(Coursera)를 정리한 내용입니다.
- Model Representation

위의 그래프는 집 크기에 따른 가격을 나타낸 것이고, 1250 feet^2의 집의 적합한 가격을 추측한다고 가정해보자. 이런 상황에서 우리는 데이터에 맞는 모델을 찾기 위해 직선을 하나 그어서 그에 대응하는 가격을 추측할 수 있다. 이러한 예시가 지난 강의에서 다루었던 Supervised Learning(지도학습) 중 Regression(회귀)의 예시 중의 하나이다. 이러한 모델을 통해서 우리는 1250 feet^2에 해당하는 적합한 가격이 220,000달러라고 말할 수 있다.
이것이 Supervised Learning이라고 불리는 이유는 데이터 예시(each example in the data)에 적합한 정답(right answer)을 도출하기 때문이다.

위의 표와 같이 우리에게 주어지는 값들을 Training Set이라고 한다. 위의 예시를 적용하면 각 집 크기에 해당하는 가격의 집합을 Training Set이라고 하는 것이다. 우리는 이 Training Set을 활용하여 1250 feet^2에 해당하는 가격은 얼마인지 알아내야 한다.
우선 수학적으로 표현하기 위한 표기 방법(Notation)을 정리해보자.
- m : Number of training examples(= table row)
- x's = "Input" variable / features(특징)
- y's = "Output" variable / "target" variable
- (x, y) - one training example
- (
) - i-th training example
이제 Training Set을 활용하여 Supervised Learning의 알고리즘에 대해 알아보자.
학습 알고리즘이 있을 때, 주어진 Training Set을 Learning Algorithm에 적용을 해야한다. 그러면 Learning Algorithm은 특정 규칙을 따라 함수 h(hypothesis)를 도출한다. 이때, 우리가 원하는 새로운 값 x에 대응하는 결과값 y를 구하기 위해 h 함수에 x를 대입하고 이때 얻은 값이 우리가 원하는 적절한 값이 된다.
(h는 x에서부터 y까지의 지도이다; h maps from x's to y's)

그래서 우리는 h 함수(Hypothesis Function:가설 함수)를 어떻게 표현할 것인가 ?
우리는 h함수를 아래와 같이 표현할 것이다.
이 함수가 의미하는 것은 아래와 같은 선형함수(Linear Function)라고 예측하는 것이다. 우리는 이를 Linear regression with one variable, 또는 Univariate linear regression라고 한다(한글 표현으로는 단순 선형회귀라고 한다).

실제로는 복잡한 비선형함수를 사용하지만, 가장 간단한 선형함수를 먼저 살펴보도록 할 것이다.
- Cost Function 비용 함수
Cost Function은 주어진 데이터(Training Set)에 가장 적합한 일차 함수(선형 함수)를 알아낼 수 있게 해준다. 앞서 살펴본 가설함수(Hypothesis function)에서 우리는 매개변수(Parameter)에 해당하는 를 결정해야 한다. 우리가 선택하는 매개변수의 값에 따라서 다른 h 함수를 가지게 된다.

Linear Regression에서 우리는 아래와 같은 Training Set을 가지고 있다고 해보자. 우리는 아래와 같이 그린 직선이 자료와 얼마나 잘 일치하는지 확인해야한다.

우리는 어떻게 선택한 파라미터가 데이터와 잘 일치하는지 알 수 있을까?
우리는 주어진 데이터에서 의 값이 최소가 되는 것이 합리적이라고 할 수 있다. 다만, 오차는 음수로도 표현될 수 있기 때문에
가 최소가 되는 것이 합리적일 것이다. 실제 Training Set은 1부터 m까지 존재하기 때문에 1부터 m까지의 차이를 모두 합해서 최소가 되는
를 구해야 한다. 공식으로 나타내면 아래와 같다.
우리가 구한 J 함수가 바로 Cost Function(비용함수)이다. 이 비용함수는 Squared error cost function(제곱 오차함수) 또는 Mean Square Error(평균 제곱 오차;MSE)이라고도 불린다. 이 제곱 오차함수는 대부분의 회귀 문제에서 적절하고 통상적인 방법이지만, 다른 비용함수들(SNR, PSNR) 또한 적절하다.
(제곱의 오차를 m, 즉 Trainig Set의 개수로 나누어 평균을 구하는데 추가적으로 2를 나누어 주는 것은 후에 미분을 할 때 계산의 편리함을 위한 것이다)
[Intuition 1]
몇몇의 예제를 통해 Cost Function이 무슨 일을 하고, 왜 사용해야 하는지 접근해보자.
우선, 직관적으로 접근하기 위해서 으로 설정하여 h 함수(hypothesis function)을 단순화한다.
Training Set 또한 단순하게 (1, 1), (2, 2), (3, 3)이라고 가정해보자.

위와 같이 여러 값에 대하여 오차함수의 값들을 구하여,
을 구해 그래프를 그리면 아래와 같이 포물선 형태가 되고, 이 포물선이 최소값을 가지게 하는 Parameter
이 최적의 값(1)이다.
[Intuition 2]
이제 가 존재하는 univariate linear regression을 생각해보자.
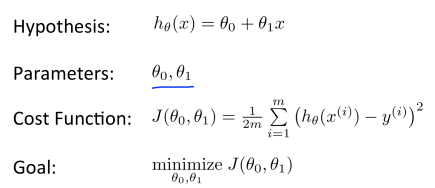
이제 파라미터가 2개가 되었고, 이전보다 비용함수 J의 그래프는 더욱 복잡해질 것이다. 마찬가지로 포물선과 같은 형태이긴 하지만 아래와 같이 3차원 그래프로 나타낼 수 있을 것이다.

이처럼 Cost Function을 표현하면 총 3가지를 표현해야하므로 위와 같이 3차원의 그래프가 된다. 우리에게 필요한 Cost Function의 값은 (x, y) 평면으로부터의 높이가 된다.
우리는 Cost Function을 더 편리하게 보기 위해서 위와 같은 3차원 도형이 아닌 3차원의 그래프를 (x, y) 평면으로 정사영시킨 등고선 그래프(Contour Plots, Contour Figures)를 활용할 것이다.

위 오른쪽 그래프가 등고선 그래프이며, 여기서 Cost Function 의 최소값은 타원의 중심좌표이다. 그리고 같은 색의 곡선은 같은 값을 갖는다.

위의 가설함수()를 살펴보면, J 함수 그래프에서 해당하는 함수는 왼쪽과 같고, 최소가 되는 그래프의 중심과 꽤 멀리 떨어져 있는 것을 볼 수 있다. 따라서 그렇게 좋은 가설함수가 아니라는 것을 예측할 수 있으며, 왼쪽 그래프를 보아도 Training Set과 많은 부분이 일치하지 않는 것을 확인할 수 있다.

위 그래프 또한, 가설함수가 Training Set들과 많은 부분이 일치하지 않고, 오른쪽 그래프에서 최소가 되는 중심이랑 많이 떨어져 있는 것을 보아 좋은 가설함수가 아니라는 것을 알 수 있다.

위 그래프는 에 대한 가설함수이다. 오른쪽 그래프의 가장 작은 타원의 중심과 인접하므로 적합한 가설함수라고 예상할 수 있고, 왼쪽 가설함수 그래프를 보니 Training Set과 비슷한 형태인 것을 확인할 수 있다.
다음 시간부터 필요한 Cost Function을 최소로 만드는
를 찾는 알고리즘에 대해 알아보자.
'Coursera 강의 > Machine Learning' 카테고리의 다른 글
| [Machine Learning] Computing Parameters Analytically (0) | 2020.08.04 |
|---|---|
| [Machine Learning] Multivariate Linear Regression (0) | 2020.08.04 |
| [Machine Learning] Gradient Descent (0) | 2020.08.04 |
| [Machine Learning] Supervised Learning/Unsupervised Learning (0) | 2020.08.02 |
| [Machine Learning] Intro / 머신러닝이란 ? (0) | 2020.08.02 |




댓글